
分析 由条件根据类比推理,由“△ABC”类比“四面体A-BCD”,“中点”类比“重心”,从而得到一个类比的命题.
解答 解:由“△ABC”类比“四面体A-BCD”,“中点”类比“重心”有,
由类比可得在四面体A-BCD中,G为△BCD的重心,则有$\overrightarrow{AG}=\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD})$,
故答案为:在四面体A-BCD中,G为△BCD的重心,则有$\overrightarrow{AG}=\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD})$.
点评 本题考查了从平面类比到空间,属于基本类比推理.利用类比推理可以得到结论、证明类比结论时证明过程与其类比对象的证明过程类似或直接转化为类比对象的结论,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
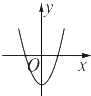 B、
B、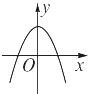 C、
C、 D、
D、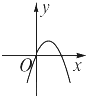
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(K2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
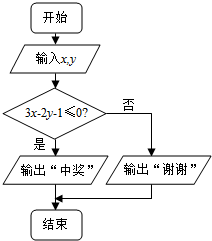 某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、200人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取10人在前排就坐,其中高二代表队有5人.
某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、200人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取10人在前排就坐,其中高二代表队有5人.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com