
| 1 |
| 8 |
| 2 |
| 8 |
| 3 |
| 8 |
| 8 |
| 8 |
| 1 |
| 8 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 8 |
| 2 |
| 8 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 8 |
| 3 |
| 8 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 8 |
| 4 |
| 8 |
| 3 |
| 4 |
| 3 |
| 2 |
| 4 |
| 8 |
| 5 |
| 8 |
| 5 |
| 4 |
| 5 |
| 2 |
| 5 |
| 8 |
| 6 |
| 8 |
| 5 |
| 4 |
| 3 |
| 2 |
| 5 |
| 2 |
| 6 |
| 8 |
| 7 |
| 8 |
| 3 |
| 2 |
| 7 |
| 4 |
| 7 |
| 2 |
| 7 |
| 8 |
| 7 |
| 4 |
| 7 |
| 2 |


科目:高中数学 来源: 题型:
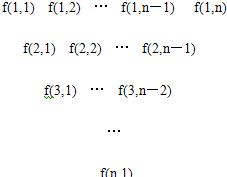 一个三角形数表按如下方式构成:第一行依次写上n(n≥4)个数,在上一行的每相邻两数的中间正下方写上这两数之和,得到下一行,依此类推.记数表中第i行的第j个数为f(i,j).
一个三角形数表按如下方式构成:第一行依次写上n(n≥4)个数,在上一行的每相邻两数的中间正下方写上这两数之和,得到下一行,依此类推.记数表中第i行的第j个数为f(i,j).| 1 |
| aiai+1 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源:2012届江西省六校高三联考数学理科试卷 题型:选择题
已知集合A={1, 2, 3, 4},函数f(x)的定义域、值域都是A,且对于任意 ,
, ,设
,设 1,
1,  2,
2,
 3,
3,
 4是1,2,3,4的任意一个排列,定义数表
4是1,2,3,4的任意一个排列,定义数表




 ,若两个数表的对应位置上至少有一个数不同,就说这是两张不同的数表,那么满足条件的不同的数表的张数为( )
,若两个数表的对应位置上至少有一个数不同,就说这是两张不同的数表,那么满足条件的不同的数表的张数为( )
A.216 B.108 C.48 D.24
查看答案和解析>>
科目:高中数学 来源:北京模拟题 题型:单选题
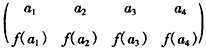 ,若两个数表的对应位置上至少有一个数不同,就说这是两张不同的数表,那么满足条件的不同的数表的张数为
,若两个数表的对应位置上至少有一个数不同,就说这是两张不同的数表,那么满足条件的不同的数表的张数为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com