
如图,在四棱锥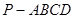 中,底面
中,底面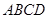 为矩形,
为矩形,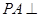 底面
底面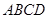 ,
,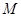 、
、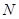 分别是
分别是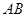 、
、 中点.
中点. 
(1)求证: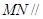 平面
平面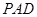 ;
;
(2)求证: .
.
(1)参考解析;(2)参考解析
解析试题分析:(1)要证直线与平面平行,根据直线与平面平行的判定定理,需要在平面内找一条直线与已知直线平行,由于本小题中点较多,所以想到作出四边形AMNQ.通过判定平行四边形,然后再用平行四边形的性质得到所需要的两直线平行,这种方法也是在证明直线与平面平行时的常用的方法.
(2)直线与直线垂直的证明根据判断定理,一般需要转化为证明直线与平面的垂直.这题是根据第一步的结论证明AB与平面PAD垂直,从而可得结论.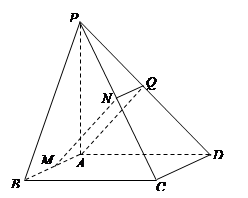
试题解析:证明:(1)取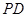 中点
中点 ,连结
,连结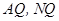 .
.
因为 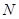 是
是 中点,
中点,
所以 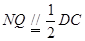 .
.
又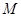 是
是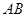 中点,
中点,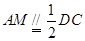 ,
,
所以 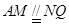 ,
,
四边形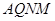 是平行四边形.所以
是平行四边形.所以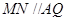 .因为
.因为 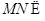 平面
平面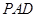 ,
,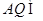 平面
平面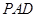 ,
,
所以 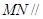 平面
平面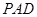 . 7分
. 7分
(2)因为 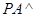 平面
平面 ,所以
,所以 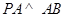 .
.
又  是矩形,
是矩形,
所以 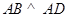 .
.
所以 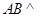 平面
平面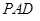 ,
,
所以 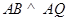 .又
.又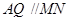 ,
,
所以 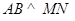 .
.
考点:1.直线与平面平行的判断定理.2.直线与直线垂直的判断方法.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:解答题
如图,四边形ABEF和ABCD都是直角梯形,∠BAD=∠FAB=90°,BC∥=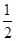 AD,BE∥=
AD,BE∥=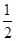 FA,G、H分别为FA、FD的中点.
FA,G、H分别为FA、FD的中点.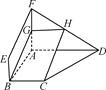
(1)证明:四边形BCHG是平行四边形.
(2)C、D、F、E四点是否共面?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在直三棱柱ABCA1B1C1中,已知∠ACB=90°,M为A1B与AB1的交点,N为棱B1C1的中点,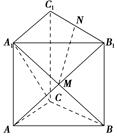
(1)求证:MN∥平面AA1C1C;
(2)若AC=AA1,求证:MN⊥平面A1BC.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在四棱台ABCD-A1B1C1D1中,D1D⊥平面ABCD,底面ABCD是平行四边形,AB=2AD,AD=A1B1,∠BAD=60°.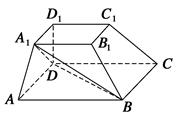
(1)证明:AA1⊥BD;
(2)证明:CC1∥平面A1BD.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,四边形ABCD为矩形,AD  平面ABE,AE=EB=BC=2,F为CE上的点.且BF
平面ABE,AE=EB=BC=2,F为CE上的点.且BF  平面ACE.
平面ACE.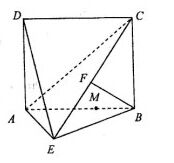
(1)求证:平面ADE 平面BCE;
平面BCE;
(2)求四棱锥E-ABCD的体积;
(3)设M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,使得MN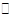 平面DAE.
平面DAE.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图:PA⊥平面ABCD,ABCD是矩形,PA=AB=1,AD=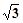 ,点F是PB的中点,点E在边BC上移动
,点F是PB的中点,点E在边BC上移动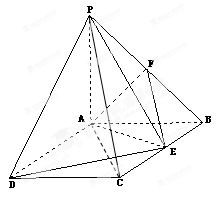
(Ⅰ)求三棱锥E-PAD的体积;
(Ⅱ)当点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(Ⅲ)证明:无论点E在边BC的何处,都有PE⊥AF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com