
分析 (Ⅰ)先求出焦点进而求出P,从而求出抛物线的方程;
(Ⅱ)先根据抛物线的焦点坐标和直线的倾斜角可表示出直线AB的方程,然后联立直线方程与抛物线方程可得到两根之和与两根之积,进而可得到中点C的横坐标
解答 解:(Ⅰ)∵抛物线y2=2px(p>0)的焦点F位于直线x+y-1=0上,
∴F(1,0)
∴抛物线方程为y2=4x;
(Ⅱ)抛物线y2=4x的焦点坐标为(1,0),准线方程为x=-1,
直线AB的方程为y=x-1,
设点A(x1,y1)、B(x2,y2).
将y=x-1代入y2=4x得x2-6x+1=0.
则x1+x2=6,x1•x2=1.
故中点C的横坐标为3.
点评 本题主要考查直线与抛物线的综合问题和两点间的距离公式.直线与圆锥曲线的综合问题一直都是高考的重点,要着重复习.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
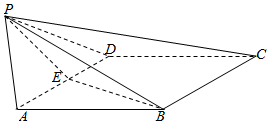 如图,四棱锥P-ABCD的侧面PAD是正三角形,底面ABCD为菱形,A点E为AD的中点,若BE=PE.
如图,四棱锥P-ABCD的侧面PAD是正三角形,底面ABCD为菱形,A点E为AD的中点,若BE=PE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正四棱锥S-ABCD的底面边长为2,E,F分别为SA,SD的中点.
如图,正四棱锥S-ABCD的底面边长为2,E,F分别为SA,SD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4-ln3 | B. | 8-ln3 | C. | 4+ln3 | D. | 8+ln3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 广告费用x(万元) | 2 | 3 | 4 | 5 | 6 |
| 销售量y(万件) | 5 | 7 | 8 | 9 | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0>1,$\sqrt{{x}_{0}}$≤1 | B. | ?x0>1,$\sqrt{{x}_{0}}$≤1 | C. | ?x0≤1,$\sqrt{{x}_{0}}$≤1 | D. | ?x0≤1,$\sqrt{{x}_{0}}$≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 27 | B. | 26 | C. | 25 | D. | 24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com