
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010-2011年福建省高二下学期学段考试数学文卷 题型:填空题
在研究身高和体重的关系时,求得相关指数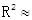 ______________,可以叙述为“身高解释了64%的体重变化,而随机误差贡献了剩余的36%”所以身高对体重的效应比随机误差的效应大得多。
______________,可以叙述为“身高解释了64%的体重变化,而随机误差贡献了剩余的36%”所以身高对体重的效应比随机误差的效应大得多。
查看答案和解析>>
科目:高中数学 来源:2007年广东省广州市增城市高二数学测试卷(文科)(选修1-2)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com