[题目]已知点.圆.点是圆上一动点. 的垂直平分线与交于点.(1)求点的轨迹方程,(2)设点的轨迹为曲线.过点且斜率不为0的直线与交于两点.点关于轴的对称点为.证明直线过定点.并求面积的最大值. 题目和参考答案——青夏教育精英家教网—

【题目】已知点，圆，点是圆上一动点，的垂直平分线与交于点.

（1）求点的轨迹方程；

（2）设点的轨迹为曲线，过点且斜率不为0的直线与交于两点，点关于轴的对称点为，证明直线过定点，并求面积的最大值.

【答案】(1) .(2) .

【解析】【试题分析】（1）由于，所以的轨迹为椭圆，利用椭圆的概念可求得椭圆方程.（2）当直线的斜率存在时，设出直线方程和点的坐标，联立直线方程和椭圆方程，写出韦达定理，求得直线的方程，求得其纵截距为，即过.验证当斜率不存在是也过.求出三角形面积的表达式并利用基本不等式求得最大值.

【试题解析】

解：（1）由已知得：，所以

又,所以点的轨迹是以为焦点，长轴长等于4的椭圆，

所以点轨迹方程是.

（2）当存在时，设直线，，则，

联立直线与椭圆得，

得，

∴，

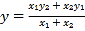∴，所以直线，

所以令，得，

，

所以直线过定点，（当不存在时仍适合）

所以的面积，当且仅当时，等号成立.

所以面积的最大值是.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图，在平面直角坐标系中，点，直线，设圆的半径为1，圆心在上.

（1）若圆心也在直线上，过点作圆的切线，求切线方程；

（2）若圆上存在点，使，求圆心的横坐标的取值范围.

查看答案和解析>>

科目：高中数学 来源： 题型：

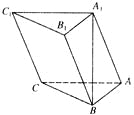
【题目】如图，在三棱柱中，，顶点在底面上的射影恰为点，且

（1）证明：平面平面；

（2）求棱与所成的角的大小；

（3）若点为的中点，并求出二面角的平面角的余弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设P是抛物线y2=4x上的一个动点，F为抛物线的焦点，记点P到点A（-1,1）的距离与点P到直线x= - 1的距离之和的最小值为M，若B（3,2），记|PB|+|PF|的最小值为N，则M+N= ______________

查看答案和解析>>

科目：高中数学 来源： 题型：

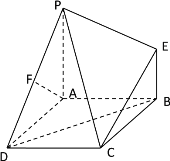
【题目】如图，四边形ABCD是正方形，PA平面ABCD，EB//PA,AB=PA=4，EB=2，F为PD的中点.

（1）求证AFPC

（2）BD//平面PEC

（3）求二面角D-PC-E的大小

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某中学作为蓝色海洋教育特色学校，随机抽取100名学生，进行一次海洋知识测试，按测试成绩(假设考试成绩均在[65，90)内)分组如下：第一组[65，70)，第二组 [70，75)，第三组[75，80)，第四组 [80，85)，第五组 [85，90)．得到频率分布直方图如图C34.

(1)求测试成绩在[80，85)内的频率；

(2)从第三、四、五组学生中用分层抽样的方法抽取6名学生组成海洋知识宣讲小组，定期在校内进行义务宣讲，并在这6名学生中随机选取2名参加市组织的蓝色海洋教育义务宣讲队，求第四组至少有1名学生被抽中的概率．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】下图是某省从1月21日至2月24日的新冠肺炎每日新增确诊病例变化曲线图.

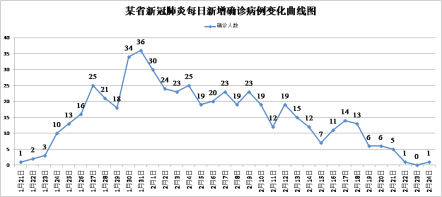
若该省从1月21日至2月24日的新冠肺炎每日新增确诊人数按日期顺序排列构成数列，的前n项和为，则下列说法中正确的是（）

A.数列是递增数列B.数列是递增数列

C.数列的最大项是D.数列的最大项是

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】【2018届河南省南阳市第一中学高三上学期第八次考试】某校在一次期末数学测试中，为统计学生的考试情况，从学校的2000名学生中随机抽取50名学生的考试成绩，被测学生成绩全部介于60分到140分之间(满分150分)，将统计结果按如下方式分成八组：第一组[60,70)，第二组[70,80)，……，第八组：[130,140]，如图是按上述分组方法得到的频率分布直方图的一部分．