
【题目】如图是函数y=f(x)的导函数y=f′(x)的图象,则下面判断正确的是( )
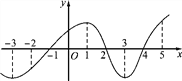
A. 在(-2,1)上f(x)是增函数 B. 在(1,3)上f(x)是减函数
C. 当x=2时,f(x)取极大值 D. 当x=4时,f(x)取极大值
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图,则下面结论中不正确的是( )


建设前经济收入构成比例 建设后经济收入构成比例
A. 新农村建设后,养殖收入增加了一倍
B. 新农村建设后,其他收入增加了一倍以上
C. 新农村建设后,种植收入减少
D. 新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的对称轴方程;
的对称轴方程;
(2)将函数![]() 的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移
的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象.若
的图象.若![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() △三个内角
△三个内角![]() ,
, ![]() ,
, ![]() 的对边,
的对边, ![]() ,
, ![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式;
(2)若f(x)在区间[2a,a+1]上不单调,求实数a的取值范围;
(3)在区间[-1,1]上,y=f(x)的图象恒在y=2x+2m+1的图象上方,试确定实数m的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分,(1)小问7分,(2)小问5分)
设函数![]()
(1)若![]() 在
在![]() 处取得极值,确定
处取得极值,确定![]() 的值,并求此时曲线
的值,并求此时曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() 在
在![]() 上为减函数,求
上为减函数,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知矩形![]() 的长为
的长为![]() ,宽为
,宽为![]() ,
, ![]() 、
、![]() 边分别在
边分别在![]() 轴、
轴、![]() 轴的正半轴上,
轴的正半轴上, ![]() 点与坐标原点重合.将矩形折叠,是
点与坐标原点重合.将矩形折叠,是![]() 点落在线段
点落在线段![]() 上.
上.
(Ⅰ)当![]() 点落在
点落在![]() 中点时,求折痕所在的直线方程.
中点时,求折痕所在的直线方程.
(Ⅱ)若折痕所在直线的斜率为![]() ,求折痕所在的直线方程与
,求折痕所在的直线方程与![]() 轴的交点坐标.(答案中可以出现
轴的交点坐标.(答案中可以出现![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com