
【题目】已知函数![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的单调性和极值;
的单调性和极值;
(Ⅱ)若函数![]() 至少有1个零点,求
至少有1个零点,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,极小值为-2,无极大值 (Ⅱ)
上单调递增,极小值为-2,无极大值 (Ⅱ)![]()
【解析】
(Ⅰ)求导得到![]() ,分别得到当
,分别得到当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,判断出
,判断出![]() 单调性,从而得到其极值;
单调性,从而得到其极值;
(Ⅱ)根据题意得到![]() ,令
,令![]() ,求导得到
,求导得到![]() ,由
,由![]() 得
得![]() ,令
,令![]() ,由零点存在定理得到存在
,由零点存在定理得到存在![]() ,使得
,使得![]() ,由
,由![]() 得到
得到![]() 的最小值,再对
的最小值,再对![]() 的零点进行分类讨论,得到答案.
的零点进行分类讨论,得到答案.
(Ⅰ)当![]() 时,
时,![]() ,
,
∴![]()
当![]() 时,
时,![]() ,
,![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
∴![]()
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
![]() 在
在![]() 处取得极小值,极小值为
处取得极小值,极小值为![]() ,无极大值
,无极大值
(Ⅱ)∵![]() ,
,
由![]() 得
得![]()
令![]() ,
,
则![]()
由![]() 得
得![]() .
.
令![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 单调递增,
单调递增,
∵![]() ,
,![]() ,
,
∴存在![]() ,使得
,使得![]()
且当![]() 时,
时,![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,即
,即![]()
∵![]() ,
,![]() ,
,
∴当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
∴![]() 在
在![]() 处取得最小值
处取得最小值![]()
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]()
∴当![]() 时,函数
时,函数![]() 无零点,
无零点,
当![]() 时,∵
时,∵![]() ,
,
∴函数![]() 至少有1个零点,
至少有1个零点,
故![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】为了促进我国人口均衡发展,从2016年1月1日起,全国统一实施全面放开二孩政策,这也是为了重建大国人口观,重新认识人口价值、人口规律、人口问题,某研究机构为了了解人们对全面放开生育二孩政策的态度,随机调查了200人,得到的统计数据如下面的不完整的2×2列联表所示(单位:人):
支持生育二孩 | 不支持生育二孩 | 合计 | |
男性 | 30 | ||
女性 | 60 | 100 | |
合计 | 70 |
(1)完成2×2列联表,并求是否有90%的把握认为是否“支持生育二孩”与性别有关?
(2)现从样本中的女性中利用分层抽样的方法抽取5人,再从这5人中随机选出2人进行深层次的交流,求选出的2人中至少有1人“支持生育二孩”的概率.
参考公式: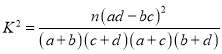 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
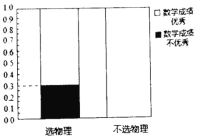
【题目】某省即将实行新高考,不再实行文理分科.某校为了研究数学成绩优秀是否对选择物理有影响,对该校2018级的1000名学生进行调查,收集到相关数据如下:
(1)根据以上提供的信息,完成![]() 列联表,并完善等高条形图;
列联表,并完善等高条形图;
选物理 | 不选物理 | 总计 | |
数学成绩优秀 | |||
数学成绩不优秀 | 260 | ||
总计 | 600 | 1000 |
(2)能否在犯错误的概率不超过0.05的前提下认为数学成绩优秀与选物理有关?
附: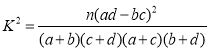
临界值表:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第41届世界博览会于2010年5月1日至10月31日,在中国上海举行,气势磅礴的中国馆——“东方之冠”令人印象深刻,该馆以“东方之冠,鼎盛中华,天下粮仓,富庶百姓”为设计理念,代表中国文化的精神与气质.其形如冠盖,层叠出挑,制似斗拱.它有四根高33.3米的方柱,托起斗状的主体建筑,总高度为60.3米,上方的“斗冠”类似一个倒置的正四棱台,上底面边长是139.4米,下底面边长是69.9米,则“斗冠”的侧面与上底面的夹角约为( ).

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为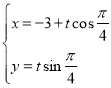 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知点![]() 是曲线
是曲线![]() 上的任意一点,当点
上的任意一点,当点![]() 到直线
到直线![]() 的距离最大时,求经过点
的距离最大时,求经过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,![]() ,
,![]() ,直线AG,BG相交于点G,且它们的斜率之积为
,直线AG,BG相交于点G,且它们的斜率之积为![]() .记点G的轨迹为曲线C.
.记点G的轨迹为曲线C.
(1)若射线![]() 与曲线C交于点D,且E为曲线C的最高点,证明:
与曲线C交于点D,且E为曲线C的最高点,证明:![]() .
.
(2)直线![]() 与曲线C交于M,N两点,直线AM,AN与y轴分别交于P,Q两点.试问在x轴上是否存在定点T,使得以PQ为直径的圆恒过点T?若存在,求出T的坐标;若不存在,请说明理由.
与曲线C交于M,N两点,直线AM,AN与y轴分别交于P,Q两点.试问在x轴上是否存在定点T,使得以PQ为直径的圆恒过点T?若存在,求出T的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某校冬季长跑活动中,学校要给获得一、二等奖的学生购买奖品,要求花费总额不得超过![]() 元.已知一等奖和二等奖奖品的单价分别为
元.已知一等奖和二等奖奖品的单价分别为![]() 元、
元、![]() 元,一等奖人数与二等奖人数的比值不得高于
元,一等奖人数与二等奖人数的比值不得高于![]() ,且获得一等奖的人数不能少于
,且获得一等奖的人数不能少于![]() 人,那么下列说法中错误的是( )
人,那么下列说法中错误的是( )
A.最多可以购买![]() 份一等奖奖品
份一等奖奖品
B.最多可以购买![]() 份二等奖奖品
份二等奖奖品
C.购买奖品至少要花费![]() 元
元
D.共有![]() 种不同的购买奖品方案
种不同的购买奖品方案
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com