
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| F1O |
| PM |
| ||||
|
|
| ||||
|
|
| B2A |
| B2B |
| B1A |
| B1B |
| |PF2| |
| |PM| |
| 2a+c |
| c |
| B2A |
| B2B |
| 6k |
| k2-3 |
| 18 |
| k2-3 |
| B1A |
| B1B |
| |PF2| |
| |PM| |
| 2a+c |
| c |
| 1 |
| e |
| c |
| a |
| 3 |
| 4 |
| a2 |
| 3 |
| 3a2 |
| x2 |
| 3 |
| y2 |
| 9 |
| B2A |
| B2B |
| 6k |
| k2-3 |
| 18 |
| k2-3 |
| B1A |
| B1B |
| 5 |
| 5 |


 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x2 |
| a2 |
| y2 |
| b2 |
| F1O |
| PM |
| OP |
| ||
|
|
| ||
|
|
A��
| ||
B��
| ||
| C��2 | ||
| D��3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
(��������14��) ��F1��F2Ϊ˫����![]() �����ҽ��㣬OΪ����ԭ�㣬P��˫������֧�ϣ�M�������ϣ�������
�����ҽ��㣬OΪ����ԭ�㣬P��˫������֧�ϣ�M�������ϣ�������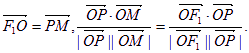 �������˫���ߵ������ʣ���������˫���߹���
�������˫���ߵ������ʣ���������˫���߹���![]() ����˫���߷��̣������裨����˫���ߵ�����˵�ΪB1��B2��B1��y���������ϣ�����B2��ֱ��AB��˫���߽���A��B���㣬��
����˫���߷��̣������裨����˫���ߵ�����˵�ΪB1��B2��B1��y���������ϣ�����B2��ֱ��AB��˫���߽���A��B���㣬��![]() ʱ��ֱ��AB�ķ���.
ʱ��ֱ��AB�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 =
=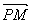 .
.

(1)��˫���ߵ�������;
(2)��˫���߹���N(2,![]() ),��˫���ߵķ���.
),��˫���ߵķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011������ʡ������ѧһ�ָ�ϰ�½���ϰ��˫���ߣ������棩 ���ͣ�ѡ����
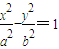 �����ҽ��㣬OΪ����ԭ�㣬��P��˫���ߵ���֧�ϣ���M��˫���ߵ������ϣ�������
�����ҽ��㣬OΪ����ԭ�㣬��P��˫���ߵ���֧�ϣ���M��˫���ߵ������ϣ������� ���ˣ�0�������˫���ߵ�������Ϊ�� ��
���ˣ�0�������˫���ߵ�������Ϊ�� ��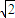

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com