
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点. 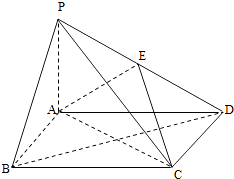
(1)证明:PB∥平面AEC;
(2)设AP=1,AD= ![]() ,三棱锥P﹣ABD的体积V=
,三棱锥P﹣ABD的体积V= ![]() ,求A到平面PBC的距离.
,求A到平面PBC的距离.
【答案】
(1)证明:设BD与AC 的交点为O,连结EO,
∵ABCD是矩形,
∴O为BD的中点
∵E为PD的中点,
∴EO∥PB.
EO平面AEC,PB平面AEC
∴PB∥平面AEC;
(2)解:∵AP=1,AD= ![]() ,三棱锥P﹣ABD的体积V=
,三棱锥P﹣ABD的体积V= ![]() ,
,
∴V= ![]() =
= ![]() ,
,
∴AB= ![]() ,PB=
,PB= ![]() =
= ![]() .
.
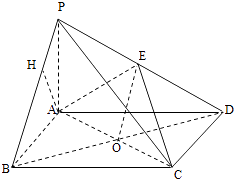
作AH⊥PB交PB于H,
由题意可知BC⊥平面PAB,
∴BC⊥AH,
故AH⊥平面PBC.
又在三角形PAB中,由射影定理可得: ![]()
A到平面PBC的距离 ![]() .
.
【解析】(1)设BD与AC 的交点为O,连结EO,通过直线与平面平行的判定定理证明PB∥平面AEC;(2)通过AP=1,AD= ![]() ,三棱锥P﹣ABD的体积V=
,三棱锥P﹣ABD的体积V= ![]() ,求出AB,作AH⊥PB角PB于H,说明AH就是A到平面PBC的距离.通过解三角形求解即可.
,求出AB,作AH⊥PB角PB于H,说明AH就是A到平面PBC的距离.通过解三角形求解即可.


科目:高中数学 来源: 题型:
【题目】已知f(x)为定义在R上的偶函数,当x≥0时,有f(x+3)=﹣f(x),且当x∈[0,3)时,f(x)=log4(x+1),给出下列命题:
①f(2015)>f(2014);
②函数f(x)在定义域上是周期为3的函数;
③直线x﹣3y=0与函数f(x)的图象有2个交点;
④函数f(x)的值域为[0,1).
其中不正确的命题个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 关于直线
关于直线![]() 对称的圆为
对称的圆为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与圆
与圆![]() 交于
交于![]() 两点,
两点, ![]() 是坐标原点,是否存在这样的直线
是坐标原点,是否存在这样的直线![]() ,使得在平行四边形
,使得在平行四边形![]() 中
中![]() ?若存在,求出所有满足条件的直线
?若存在,求出所有满足条件的直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx+1(a,b∈R且a≠0),F(x)= ![]() .
.
(1)若f(﹣1)=0,且函数f(x)的值域为[0,+∞),求F(x)的解析式;
(2)在(1)的条件下,当x∈[﹣2,2]时,g(x)=f(x)﹣kx是单调函数,求实数k的取值范围;
(3)设mn<0,m+n>0,a>0,且f(x)是偶函数,判断F(m)+F(n)是否大于零.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C的对边分别为a,b,c,b=2 ![]() ,B=
,B= ![]() .
.
(1)若a=2,求角C;
(2)若D为AC的中点,BD= ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“累计净化量(CCM)”是空气净化器质量的一个重要衡量指标,它是指空气净化器从开始使用到净化效率为![]() 时对颗粒物的累计净化量(单位:克).根据国家标准,对空气净化器的累计净化量(CCM)有如下等级划分:
时对颗粒物的累计净化量(单位:克).根据国家标准,对空气净化器的累计净化量(CCM)有如下等级划分:
累计净化量(克) |
|
|
| 12以上 |
等级 |
|
|
|
|
已知某批空气净化器共![]() 台,其累计净化量都分布在区间
台,其累计净化量都分布在区间![]() 内,为了解其质量,随机抽取了
内,为了解其质量,随机抽取了![]() 台净化器作为样本进行估计,按照
台净化器作为样本进行估计,按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 均匀分组,其中累计净化量在
均匀分组,其中累计净化量在![]() 的所有数据有:
的所有数据有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 和
和![]() ,并绘制了如下频率分布直方图.
,并绘制了如下频率分布直方图.
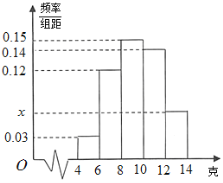
(1)求![]() 的值及频率分布直方图中
的值及频率分布直方图中![]() 的值;
的值;
(2)以样本估计总体,试估计这批空气净化器(共2000台)中等级为![]() 的空气净化器有多少台?
的空气净化器有多少台?
(3)从累计净化量在![]() 的样本中随机抽取2台,求恰好有1台等级为
的样本中随机抽取2台,求恰好有1台等级为![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】采用系统抽样方法从960人中抽取32人做问卷调查,为此将他们随即编号为1,2…960,分组后在第一组采用简单随机抽样的方法抽到的号码为5,抽到的32人中,编号落入区间[1,450]的人做问卷A,编号落入区间[451,750]的人做问卷B,其余的人做问卷C,则抽到的32人中,做问卷C的人数为( )
A.15
B.10
C.9
D.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x3﹣2ax2+3x(x∈R).
x3﹣2ax2+3x(x∈R).
(1)若a=1,点P为曲线y=f(x)上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程;
(2)若函数y=f(x)在(0,+∞)上为单调增函数,试求满足条件的最大整数a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
(1)命题“若 ![]() ,则tanα=1”的逆否命题为假命题;
,则tanα=1”的逆否命题为假命题;
(2)命题p:x∈R,sinx≤1.则¬p:x0∈R,使sinx0>1;
(3)“ ![]() ”是“函数y=sin(2x+)为偶函数”的充要条件;
”是“函数y=sin(2x+)为偶函数”的充要条件;
(4)命题p:“x0∈R,使 ![]() ”;命题q:“若sinα>sinβ,则α>β”,那么(¬p)∧q为真命题.
”;命题q:“若sinα>sinβ,则α>β”,那么(¬p)∧q为真命题.
其中正确的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com