
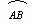
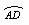
(1) (2)
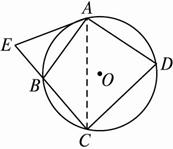
图2-4-18
(1)求证:AB·DA=CD·BE;
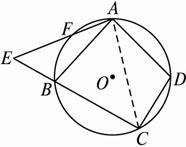
(2)如图2-4-18(2),若点E在CB延长线上运动,使切线EA变为割线EFA,其他条件不变,问具备什么条件使原结论成立?
思路分析:(1)只需证△ABE∽△CDA.?
(2)如题图(2),要使结论仍然成立,注意到∠ABE =∠ADC始终成立,因此仍然只需使△ABE∽△CDA即可,这样只要另一组对应角相等即可,即只需∠BAE =∠ACD或∠E =∠CAD.
(1)证明:连结AC,∵AE切⊙O于A,?
∴∠EAB =∠ACB.?
∵![]() =
=![]() ,?
,?
∴∠ACD =∠ACB.?
∴∠EAB =∠ACD.?
又∵四边形ABCD内接于⊙O,?
∴∠ABE =∠CDA.∴△ABE∽△CDA.?
∴![]() =
=![]() .∴AB·DA =CD·BE.
.∴AB·DA =CD·BE.
(2)解:当![]() =
=![]() 时,∠EAB =∠ACD,
时,∠EAB =∠ACD,
又∠ABE =∠ADC,?
∴△ABE∽△ACD,?
∴AB·DA =CD·BE,此时仍然成立.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
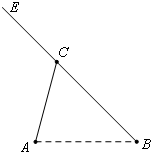 如图,A,B,C是三个汽车站,AC,BE是直线型公路.已知AB=120km,∠BAC=75°,∠ABC=45°.有一辆车(称甲车)以每小时96(km)的速度往返于车站A,C之间,到达车站后停留10分钟;另有一辆车(称乙车)以每小时120(km)的速度从车站B开往另一个城市E,途经车站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出.
如图,A,B,C是三个汽车站,AC,BE是直线型公路.已知AB=120km,∠BAC=75°,∠ABC=45°.有一辆车(称甲车)以每小时96(km)的速度往返于车站A,C之间,到达车站后停留10分钟;另有一辆车(称乙车)以每小时120(km)的速度从车站B开往另一个城市E,途经车站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出.| 2 |
| 3 |
| 6 |
| 331 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:

图
(1)当∠QPA=60°时,请你对△QCP的形状作出猜想,并证明;
(2)当QP⊥AO时,△QCP的形状是___________三角形.
(3)由(1)、(2)得出的结论,请你进一步猜想,当点P在线段AM上运动到任何位置时△QCP一定是___________三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com