
【题目】如图,已知二次函数y=x2+bx+c过点A(1,0),C(0,﹣3)
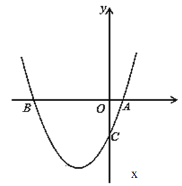
(1)求此二次函数的解析式;
(2)在抛物线上存在一点P使△ABP的面积为10,求点P的坐标.
【答案】(1)y=x2+2x﹣3(2)P(﹣4,5)(2,5)
【解析】
试题分析:(1)利用待定系数法把A(1,0),C(0,-3)代入二次函数y=x2+bx+c中,即可算出b、c的值,进而得到函数解析式是y=x2+2x-3;(2)首先求出A、B两点坐标,再算出AB的长,再设P(m,n),根据△ABP的面积为10可以计算出n的值,然后再利用二次函数解析式计算出m的值即可得到P点坐标
试题解析:(1)∵二次函数y=x2+bx+c过点A(1,0),C(0,﹣3),
∴![]() ,解得
,解得![]() ,
,
∴二次函数的解析式为y=x2+2x﹣3;
(2)∵当y=0时,x2+2x﹣3=0,解得:x1=﹣3,x2=1;
∴A(1,0),B(﹣3,0),∴AB=4,
设P(m,n),∵△ABP的面积为10,∴![]() AB|n|=10,解得:n=±5,
AB|n|=10,解得:n=±5,
当n=5时,m2+2m﹣3=5,解得:m=﹣4或2,∴P(﹣4,5)(2,5);
当n=﹣5时,m2+2m﹣3=﹣5,方程无解,
故P(﹣4,5)(2,5);


科目:高中数学 来源: 题型:
【题目】 用反证法证明命题:“三角形三个内角至少有一个不大于60°”时,应假设( )
A.三个内角都不大于60° B.三个内角都大于60°
C.三个内角至多有一个大于60° D.三个内角至多有两个大于60°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.

(1)证明:![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)设点![]() 在线段
在线段![]() 上,且直线
上,且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,当点
,当点![]() 在
在![]() 的图象上运动时,点
的图象上运动时,点![]() 在函数
在函数![]() 的图象上运动(
的图象上运动(![]() ).
).
(Ⅰ)求![]() 和
和![]() 的表达式;
的表达式;
(Ⅱ)已知关于![]() 的方程
的方程![]() 有实根,求实数
有实根,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)设![]() ,函数
,函数![]() 的值域为
的值域为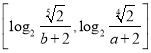 ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为打入国际市场,决定从![]() 、
、![]() 两种产品中只选择一种进行投资生产,已知投资生产这两种产品的有关数据如下表:(单位:万美元)
两种产品中只选择一种进行投资生产,已知投资生产这两种产品的有关数据如下表:(单位:万美元)
年固定成本 | 每件产品成本 | 每件产品销售价 | 每年最多可生产的件数 | |
A产品 | 20 |
| 10 | 200 |
B产品 | 40 | 8 | 18 | 120 |
其中年固定成本与年生产的件数无关,![]() 是待定常数,其值由生产
是待定常数,其值由生产![]() 产品的原材料决定,预计
产品的原材料决定,预计![]() ,另外,年销售
,另外,年销售![]() 件B产品时需上交
件B产品时需上交![]() 万美元的特别关税,假设生产出来的产品都能在当年销售出去.
万美元的特别关税,假设生产出来的产品都能在当年销售出去.
(1)求该厂分别投资生产A、![]() 两种产品的年利润
两种产品的年利润![]() 与生产相应产品的件数
与生产相应产品的件数![]() 之间的函数关系,并求出其定义域;
之间的函数关系,并求出其定义域;
(2)如何投资才可获得最大年利润?请设计相关方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产的一种电子产品的成本是每件500元,计划在今后的3年内,使成本降低到每件256元,则平均每年成本应降低( )
A. 10% B. 15% C. 20% D. 25%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解高一新生数学科学习情况,用系统抽样方法从编号为001,002,003,…,700的学生中抽取14人,若抽到的学生中编号最大的为654,则被抽到的学生中编号最小的为( )
A. 002 B. 003 C. 004 D. 005
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com