练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】2010-2018年之间，受益于基础设施建设对光纤产品的需求，以及个人计算机及智能手机的下一代规格升级，电动汽车及物联网等新机遇，连接器行业增长呈现加速状态．根据该折线图，下列结论正确的个数为（ ）

    ①每年市场规模量逐年增加；

    ②增长最快的一年为2013～2014；

    ③这8年的增长率约为40％；

    ④2014年至2018年每年的市场规模相对于2010年至2014年每年的市场规模，数据方差更小，变化比较平稳

    A. 1B. 2C. 3D. 4

    【答案】C

    【解析】

    由题意观察所给的折线图考查所给的结论是否正确即可.

    考查所给的结论：

    ①2011-2012年的市场规模量有所下降，该说法错误；

    ②增长最快的一年为2013～2014，该说法正确；

    ③这8年的增长率约为40％，该说法正确；

    ④2014年至2018年每年的市场规模相对于2010年至2014年每年的市场规模，数据方差更小，变化比较平稳，该说法正确.

    综上可得：正确的结论有3个.

    故选：C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】用0与1两个数字随机填入如图所示的5个格子里，每个格子填一个数字，并且从左到右数，不管数到哪个格子，总是1的个数不少于0的个数，则这样填法的概率为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知为椭圆E： 的左、右顶点， ，E的两个焦点与E的短轴两个端点所构成的四边形是正方形．

    （1）求椭圆E的方程；

    （2）设动点（），记直线与E的交点（不同于）到x轴的距离分别为，求的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平行四边形OABC中，过点C的直线与线段OA、OB分别相交于点M、N，若，；（1）求y关于x的函数解析式；（2）定义函数，点列Pi（xi，F（xi））（i=1，2，…，n，n≥2）在函数y=F（x）的图象上，且数列{xn}是以1为首项，0.5为公比的等比数列，O为原点，令，是否存在点Q（1，m），使得？若存在，求出Q点的坐标，若不存在，说明理由；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线的参数方程为（为参数），以坐标原点为极点， 轴的非负半轴为极轴建立极坐标系，圆的极坐标方程为，直线与圆交于， 两点.

    （1）求圆的直角坐标方程及弦的长；

    （2）动点在圆上（不与， 重合），试求的面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，点在以为直径的圆上，垂直与圆所在平面，为的垂心.

    （1）求证：平面平面；

    （2）若，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若一个函数当自变量在不同范围内取值时，函数表达式不同，我们称这样的函数为分段函数．下面我们参照学习函数的过程与方法，探究分段函数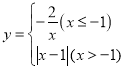的图象与性质．列表：

    x

    …

    0

    1

    2

    3

    …

    y

    …

    1

    2

    1

    0

    1

    2

    …

    描点：在平面直角坐标系中，以自变量x的取值为横坐标，以相应的函数值y为纵坐标，描出相应的点，如图所示．

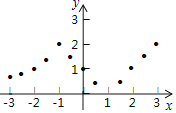
    （1）如图，在平面直角坐标系中，观察描出的这些点的分布，作出函数图象；

    （2）研究函数并结合图象与表格，回答下列问题：

    ①点，，，在函数图象上，　 　，　 　；（填“＞”，“＝”或“＜”）

    ②当函数值时，求自变量x的值；

    ③在直线的右侧的函数图象上有两个不同的点，，且，求的值；

    ④若直线与函数图象有三个不同的交点，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知下列命题：

    ①在某项测量中，测量结果服从正态分布，若在内取值范围概率为，则在内取值的概率为；

    ②若，为实数，则“”是“”的充分而不必要条件；

    ③已知命题，，则是：

    ，；

    ④中，“角，，成等差数列”是“”的充分不必要条件；其中，所有真命题的个数是（ ）

    A. 个 B. 个 C. 个 D. 个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义在R上的偶函数f(x)满足f(x＋1)＝－f(x)且f(x)在[－1,0]上是增函数，给出下列四个命题：

    ①f(x)是周期函数；②f(x)的图象关于x＝1对称；③f(x)在[1,2]上是减函数；④f(2)＝f(0)．

    其中正确命题的序号是____________．(请把正确命题的序号全部写出来)

    查看答案和解析>>

    同步练习册答案