Question

等差数列{a_n}的项数m是奇数，且a₁+a₃+…+a_m=44，a₂+a₄+…+a_m-1=33．求m的值．

Answer 1

解：∵等差数列{a_n}，a₁+a₃+…+a_m=44，a₂+a₄+…+a_m-1=33，
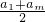
∴a₁+a₃+…+a_m=•=44①，
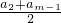
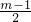
a₂+a₄+…+a_m-1=•=33②，
又a₁+a_m=a₂+a_m-1，
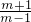
∴得：=，即4m-4=3m+3，
解得：m=7．
分析：由数列{a_n}为等差数列，利用等差数列的求和公式化简已知的两等式，再利用等差数列的性质得到a₁+a_m=a₂+a_m-1，将化简得到的两关系式左右两边相除，得到关于m的方程，求出方程的解得到m的值．
点评：此题考查了等差数列的性质，以及等差数列的前n项和公式，熟练掌握性质及公式是解本题的关键．