
【题目】在平面直角坐标系![]() 中,已知椭圆E:
中,已知椭圆E:![]() 的离心率是
的离心率是![]() ,短轴长为2,若点A,B分别是椭圆E的左右顶点,动点
,短轴长为2,若点A,B分别是椭圆E的左右顶点,动点![]() ,
,![]() ,直线
,直线![]() 交椭圆E于P点.
交椭圆E于P点.
(1)求椭圆E的方程
(2)①求证:![]() 是定值;
是定值;
②设![]() 的面积为
的面积为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1, ![]() =9a2a6.
=9a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列![]() 的前n项和.
的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆规是用来画椭圆的一种器械,它的构造如图所示,在一个十字形的金属板上有两条互相垂直的导槽,在直尺上有两个固定的滑块A,B,它们可分别在纵槽和横槽中滑动,在直尺上的点M处用套管装上铅笔,使直尺转动一周,则点M的轨迹C是一个椭圆,其中|MA|=2,|MB|=1,如图,以两条导槽的交点为原点O,横槽所在直线为x轴,建立直角坐标系.
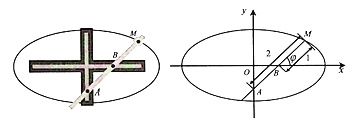
(1)将以射线Bx为始边,射线BM为终边的角xBM记为φ(0≤φ<2π),用![]() 表示点M的坐标,并求出C的普通方程;
表示点M的坐标,并求出C的普通方程;
(2)已知过C的左焦点F,且倾斜角为α(0≤α![]() )的直线l1与C交于D,E两点,过点F且垂直于l1的直线l2与C交于G,H两点.当
)的直线l1与C交于D,E两点,过点F且垂直于l1的直线l2与C交于G,H两点.当![]() ,|GH|,
,|GH|,![]() 依次成等差数列时,求直线l2的普通方程.
依次成等差数列时,求直线l2的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ,且
,且![]() ,②
,②![]() ,且
,且![]() ,③
,③![]() ,且
,且![]() 这三个条件中任选一个,补充在下面问题中,若问题中的
这三个条件中任选一个,补充在下面问题中,若问题中的![]() 存在,求出
存在,求出![]() 和数列
和数列![]() 的通项公式与前
的通项公式与前![]() 项和;若
项和;若![]() 不存在,请说明理由.
不存在,请说明理由.
设![]() 为各项均为正数的数列
为各项均为正数的数列![]() 的前
的前![]() 项和,满足________,是否存在
项和,满足________,是否存在![]() ,使得数列
,使得数列![]() 成为等差数列?
成为等差数列?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,右顶点
,右顶点![]() ,上顶点为B,左右焦点分别为
,上顶点为B,左右焦点分别为![]() ,且
,且![]() ,过点A作斜率为
,过点A作斜率为![]() 的直线l交椭圆于点D,交y轴于点E.
的直线l交椭圆于点D,交y轴于点E.
(1)求椭圆C的方程;
(2)设P为![]() 的中点,是否存在定点Q,对于任意的
的中点,是否存在定点Q,对于任意的![]() 都有
都有![]() ?若存在,求出点Q;若不存在,请说明理由.
?若存在,求出点Q;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全国文明城市是中国所有城市品牌中含金量最高、创建难度最大的一个,是反映城市整体文明水平的综合性荣誉称号,是目前国内城市综合类评比中的最高荣誉,也是最具价值的城市品牌,作为普通市民,既是城市文明的最大受益者,更是文明城市的主要创造者,皖北某市为提高市民对文明城市创建的认识,举办了“创建文明城市”知识竞赛,从所有答卷中随机抽取400份试卷作为样本,将样本的成绩(满分100分,成绩均为不低于40分的整数)分成六段:![]() 后得到如图所示的频率分布直方图.
后得到如图所示的频率分布直方图.
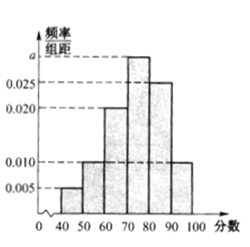
(Ⅰ)求样本的平均数;
(Ⅱ)现从该样本成绩在![]() 与
与![]() 两个分数段内的市民中按分层抽样选取6人,求从这6人中随机选取2人,且2人的竞赛成绩之差的绝对值大于20的概率.
两个分数段内的市民中按分层抽样选取6人,求从这6人中随机选取2人,且2人的竞赛成绩之差的绝对值大于20的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了对某种商品进行合理定价,需了解该商品的月销售量![]() (单位:万件)与月销售单价
(单位:万件)与月销售单价![]() (单位:元/件)之间的关系,对近
(单位:元/件)之间的关系,对近![]() 个月的月销售量
个月的月销售量![]() 和月销售单价
和月销售单价![]()
![]() 数据进行了统计分析,得到一组检测数据如表所示:
数据进行了统计分析,得到一组检测数据如表所示:
月销售单价 |
|
|
|
|
|
|
月销售量 |
|
|
|
|
|
|
(1)若用线性回归模型拟合![]() 与
与![]() 之间的关系,现有甲、乙、丙三位实习员工求得回归直线方程分别为:
之间的关系,现有甲、乙、丙三位实习员工求得回归直线方程分别为:![]() ,
,![]() 和
和![]() ,其中有且仅有一位实习员工的计算结果是正确的.请结合统计学的相关知识,判断哪位实习员工的计算结果是正确的,并说明理由;
,其中有且仅有一位实习员工的计算结果是正确的.请结合统计学的相关知识,判断哪位实习员工的计算结果是正确的,并说明理由;
(2)若用![]() 模型拟合
模型拟合![]() 与
与![]() 之间的关系,可得回归方程为
之间的关系,可得回归方程为![]() ,经计算该模型和(1)中正确的线性回归模型的相关指数
,经计算该模型和(1)中正确的线性回归模型的相关指数![]() 分别为
分别为![]() 和
和![]() ,请用
,请用![]() 说明哪个回归模型的拟合效果更好;
说明哪个回归模型的拟合效果更好;
(3)已知该商品的月销售额为![]() (单位:万元),利用(2)中的结果回答问题:当月销售单价为何值时,商品的月销售额预报值最大?(精确到
(单位:万元),利用(2)中的结果回答问题:当月销售单价为何值时,商品的月销售额预报值最大?(精确到![]() )
)
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:![]() (
(![]() )的焦点为F,过F且斜率为1的直线与C交于A,B两点,
)的焦点为F,过F且斜率为1的直线与C交于A,B两点,![]() .
.
(1)求C的方程;
(2)过点![]() 的直线l交C于点M,N,点Q为
的直线l交C于点M,N,点Q为![]() 的中点,
的中点,![]() 轴交C于点R,且
轴交C于点R,且![]() ,证明:动点T在定直线上.
,证明:动点T在定直线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com