
【题目】已知函数f(x)=ln(ax+b)﹣x(a,b∈R,ab≠0).
(1)讨论f(x)的单调性;
(2)若f(x)≤0恒成立,求ea(b﹣1)的最大值.
【答案】(1)讨论见解析;(2)最大值为0
【解析】
(1)分![]() 时,
时,![]() 时,两种情况讨论
时,两种情况讨论![]() 单调性.
单调性.
(2)由(1)知:当![]() 时,取
时,取![]() 且
且![]() 时,
时,![]() ,与题意不合,当
,与题意不合,当![]() 时,由题目中恒成立可得,
时,由题目中恒成立可得,![]() ,得
,得![]() ,所以
,所以![]() ,令
,令![]() ,只需求
,只需求![]() 即可.
即可.
(1)①当a>0时,则f(x)的定义域为(﹣![]() ,+∞),
,+∞),
![]() =
=![]() ,由f′(x)=0,
,由f′(x)=0,
得x=1﹣![]() >﹣
>﹣![]() ,
,
所以f(x)在(﹣![]() ,1﹣
,1﹣![]() )单调递增,在(1﹣
)单调递增,在(1﹣![]() ,+∞)单调递减,
,+∞)单调递减,
②当a<0时,则f(x)的定义域为(﹣∞,﹣![]() ),
),
由f′(x)=0得x=1﹣![]() >﹣
>﹣![]() ,
,
所以f(x)在(﹣∞,﹣![]() )单调递减.
)单调递减.
综上:当a>0时,f(x)在(﹣![]() ,1﹣
,1﹣![]() )单调递增,在(1﹣
)单调递增,在(1﹣![]() ,+∞)单调递减.
,+∞)单调递减.
当a<0时, f(x)在(﹣∞,﹣![]() )单调递减.
)单调递减.
(2)由(1)知:当a<0时,取x0<![]() 且x0<0时,
且x0<0时,
f(x0)>ln(a×![]() +b)﹣x0>0,与题意不合,
+b)﹣x0>0,与题意不合,
当a>0时,f(x)max=f(1﹣![]() )=lna﹣1+
)=lna﹣1+![]() ≤0,即b﹣1≤ a﹣alna﹣1,
≤0,即b﹣1≤ a﹣alna﹣1,
所以ea(b﹣1)≤(a﹣alna﹣1)ea,令h(x)=(x﹣xlnx﹣1)ex,
则h′(x)=(x﹣xlnx﹣lnx﹣1)ex,
令u(x)=x﹣xlnx﹣lnx﹣1,则u′(x)=﹣lnx﹣![]() ,
,
则u″(x)=![]() ,
,
u′(x)在(0,1)上单调递增,在(1,+∞)上单调递减.
则u′(x)max=u′(1)<0,
从而u(x)在(0,+∞)单调递减,又因为u(1)=0.
所以当x∈(0,1)时,u(x)>0,即h′(x)>0;
当x∈(1,+∞)时,u(x)<0,即h′(x)<0,
则h(x)在(0,1)单调递增,在(1,+∞)单调递减,
所以h(x)max=h(1)=0.
所以ea(b﹣1)的最大值为0.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设有二元关系![]() ,已知曲线
,已知曲线![]() .
.
(1)若![]() 时,正方形
时,正方形![]() 的四个顶点均在曲线
的四个顶点均在曲线![]() 上,求正方形
上,求正方形![]() 的面积;
的面积;
(2)设曲线![]() 与
与![]() 轴的交点是
轴的交点是![]() ,抛物线
,抛物线![]() 与
与![]() 轴的交点是
轴的交点是![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() ,求证直线
,求证直线![]() 过定点,并求该定点的坐标;
过定点,并求该定点的坐标;
(3)设曲线![]() 与
与![]() 轴的交点是
轴的交点是![]() ,
,![]() ,可知动点
,可知动点![]() 在某确定的曲线
在某确定的曲线![]() 上运动,曲线
上运动,曲线![]() 上与上述曲线
上与上述曲线![]() 在
在![]() 时共有4个交点,其坐标分别是
时共有4个交点,其坐标分别是![]() 、
、![]() 、
、![]() 、
、![]() ,集合
,集合![]() 的所有非空子集设为
的所有非空子集设为![]() ,将
,将![]() 中的所有元素相加(若
中的所有元素相加(若![]() 只有一个元素,则和是其自身)得到255个数
只有一个元素,则和是其自身)得到255个数![]() ,求所有正整数
,求所有正整数![]() 的值,使得
的值,使得![]() 是一个与变数
是一个与变数![]() 及变数
及变数![]() 均无关的常数.
均无关的常数.
查看答案和解析>>
科目:高中数学 来源: 题型:
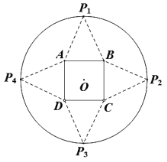
【题目】如图,圆形纸片的圆心为![]() ,半径为
,半径为![]() ,该纸片上的正方形
,该纸片上的正方形![]() 的中心为
的中心为![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() 为圆
为圆![]() 上点,
上点,![]() ,
,![]() ,
,![]() ,
,![]() 分别是以
分别是以![]() ,
,![]() ,
,![]() ,
,![]() 为底边的等腰三角形,沿虚线剪开后,分别以
为底边的等腰三角形,沿虚线剪开后,分别以![]() ,
,![]() ,
,![]() ,
,![]() 为折痕折起
为折痕折起![]() ,
,![]() ,
,![]() ,
,![]() ,使得
,使得![]() 、
、![]() 、
、![]() 、
、![]() 重合,得到四棱锥.当该四棱锥体积取得最大值时,正方形
重合,得到四棱锥.当该四棱锥体积取得最大值时,正方形![]() 的边长为______
的边长为______![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,1),抛物线C:y2=ax(a>0)的焦点为F,连接FA,与抛物线C相交于点M,延长FA,与抛物线C的准线相交于点N,若|FM|:|MN|=1:2,则实数a的值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生对函数![]() 的性质进行研究,得出如下的结论:
的性质进行研究,得出如下的结论:
![]() 函数在
函数在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
![]() 点
点![]() 是函数图象的一个对称中心;
是函数图象的一个对称中心;
![]() 函数图象关于直线
函数图象关于直线![]() 对称;
对称;
![]() 存在常数
存在常数![]() ,使
,使![]() 对一切实数x均成立,
对一切实数x均成立,
其中正确命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为数列
为数列![]() 前
前![]() 项的和,
项的和,![]()
![]() ,数列
,数列![]() 的通项公式
的通项公式![]()
![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,则称
,则称![]() 为数列
为数列![]() 与
与![]() 的公共项,将数列
的公共项,将数列![]() 与
与![]() 的公共项,按它们在原数列中的先后顺序排成一个新数列
的公共项,按它们在原数列中的先后顺序排成一个新数列![]() ,求
,求![]() 的值;
的值;
(3)是否存在正整数![]() 、
、![]() 、
、![]()
![]() 使得
使得![]() 成立,若存在,求出
成立,若存在,求出![]() 、
、![]() 、
、![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com