
分析 (1)设出B,C的坐标,利用点斜式求得直线l的方程,与抛物线方程联立消去x,利用韦达定理表示出x1+x2和x1x2,由$\overrightarrow{AC}=\frac{1}{4}\overrightarrow{AB}$.根据求得y2=4y1,最后联立方程求得y1,y2和p,则抛物线的方程可得.
(2)设直线l的方程,AB中点坐标,把直线与抛物线方程联立,利用判别式求得k的范围,利用韦达定理表示出x1+x2,进而求得x0,利用直线方程求得y0,进而可表示出AB的中垂线的方程,求得其在y轴上的截距,根据k的范围确定b的范围.
解答 解:(Ⅰ)直线l的斜率是$\frac{1}{2}$时,直线BC的方程为:x=2y-4,设B(x1,y1),C(x2,y2),
$\left\{\begin{array}{l}{{x}^{2}=2py}\\{x=2y-4}\end{array}\right.$,整理得:2y2-(8+p)y+8=0,
由韦达定理可知:y1+y2=$\frac{8+p}{2}$,y1•y2=4,
由$\overrightarrow{AC}=\frac{1}{4}\overrightarrow{AB}$.则y1=4y2,
由p>0,解得:y1=1,y2=4,
∴p=2,
∴抛物线G:x2=4y;
(Ⅱ)设l:y=k(x+4),BC中点坐标为(x0,y0)
由$\left\{\begin{array}{l}{{x}^{2}=4y}\\{y=k(x+4)}\end{array}\right.$,整理得:x2-4kx-16k=0,
∴由韦达定理可知:x1+x2=2k,则x0=$\frac{{x}_{1}+{x}_{2}}{2}$=2k.则y0=k(x0+4)=2k2+4k,
∴BC的中垂线方程为y-(2k2+4k)=-$\frac{1}{k}$(x-2k),
∴BC的中垂线在y轴上的截距为:b=2k2+4k+2=2(k+1)2,
对于方程由△=16k2+64k>0,解得:k>0或k<-4.
∴b的取值范围(2,+∞).
点评 本题主要考查抛物线的标准方程,直线与圆锥曲线的综合问题.考查判别式和韦达定理的应用,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2x-y+1=0 | B. | x-2y+1=0 | C. | 2x+y+1=0 | D. | 2x-y+2=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2)∪(2,+∞) | B. | (2,+∞) | C. | [2,+∞) | D. | (-∞,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
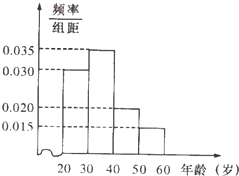 某工厂有120名工人,其年龄都在20~60岁之间,各年龄段人数按[20,30),[30,40),[40,50),[50,60)分成四组,其频率分布直方图如图所示.工厂为了开发新产品,引进了新的生产设备,要求每个工人都要参加A、B两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表所示.假设两项培训是相互独立的,结业考试也互不影响.
某工厂有120名工人,其年龄都在20~60岁之间,各年龄段人数按[20,30),[30,40),[40,50),[50,60)分成四组,其频率分布直方图如图所示.工厂为了开发新产品,引进了新的生产设备,要求每个工人都要参加A、B两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表所示.假设两项培训是相互独立的,结业考试也互不影响.| 年龄分组 | A项培训成绩优秀人数 | B项培训成绩优秀人数 |
| [20,30) | 27 | 16 |
| [30,40) | 28 | 18 |
| [40,50) | 26 | 9 |
| [50,60] | 6 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若x>1,则?y∈(-∞,1),xy≠1 | B. | 若x=sinθcosθ,则?θ∈(0,π),x≠$\frac{1}{2}$ | ||
| C. | 若x>1,则?y∈(-∞,1),xy=1 | D. | 若x=sinθcosθ,则?θ∈(0,π),x=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com