
【题目】已知a为常数,函数![]() 有两个极值点x1,x2,且x1<x2,则有( )
有两个极值点x1,x2,且x1<x2,则有( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】A
【解析】
求导f′(x)=x﹣aex,将问题转化为![]() 有两根为x1,x2,设
有两根为x1,x2,设![]() ,利用导数法研究其图象利用数形结合法求解.
,利用导数法研究其图象利用数形结合法求解.
依题意:f′(x)=x﹣aex,则f′(x)=0的两根为x1,x2,即![]() 的两根为x1,x2,
的两根为x1,x2,
设![]() ,则
,则![]() ,令g′(x)=0,解得x=1,
,令g′(x)=0,解得x=1,
∴g(x)在(﹣∞,1)上单调递增,在(1,+∞)上单调递减,函数g(x)的图象如下,

由图可知,0<x1<1,x2>1,
当x∈(﹣∞,x1)∪(x2,+∞)时,![]() ,则f′(x)<0,f(x)单调递减,
,则f′(x)<0,f(x)单调递减,
当x∈(x1,x2)时,![]() ,则f′(x)>0,f(x)单调递增,
,则f′(x)>0,f(x)单调递增,
∴f(x)极小值![]() ,又x1∈(0,1),
,又x1∈(0,1),
故![]() ,
,
f(x)极大值![]() ,又x2∈(1,+∞),
,又x2∈(1,+∞),
故![]() .
.
故选:A.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某单位年会进行抽奖活动,在抽奖箱里装有![]() 张印有“一等奖”的卡片,
张印有“一等奖”的卡片, ![]() 张印
张印
有“二等奖”的卡片, 3张印有“新年快乐”的卡片,抽中“一等奖”获奖![]() 元, 抽中“二等奖”获奖
元, 抽中“二等奖”获奖![]() 元,抽中“新年快乐”无奖金.
元,抽中“新年快乐”无奖金.
(1)单位员工小张参加抽奖活动,每次随机抽取一张卡片,抽取后不放回.假如小张一定要将所有获奖卡片全部抽完才停止. 记![]() 表示“小张恰好抽奖
表示“小张恰好抽奖![]() 次停止活动”,求
次停止活动”,求![]() 的值;
的值;
(2)若单位员工小王参加抽奖活动,一次随机抽取![]() 张卡片.
张卡片.
①![]() 记
记![]() 表示“小王参加抽奖活动中奖”,求
表示“小王参加抽奖活动中奖”,求![]() 的值;
的值;
②设![]() 表示“小王参加抽奖活动所获奖金数(单位:元)”,求
表示“小王参加抽奖活动所获奖金数(单位:元)”,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在统计学中,同比增长率一般是指和去年同期相比较的增长率,环比增长率一般是指和前一时期相比较的增长率.2020年2月29日人民网发布了我国2019年国民经济和社会发展统计公报图表,根据2019年居民消费价格月度涨跌幅度统计折线图,下列说法正确的是( )
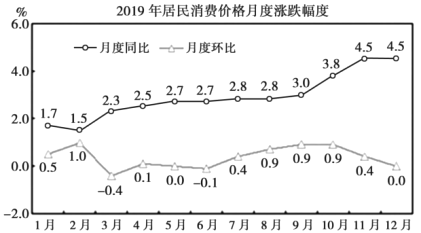
A.2019年我国居民每月消费价格与2018年同期相比有涨有跌
B.2019年我国居民每月消费价格中2月消费价格最高
C.2019年我国居民每月消费价格逐月递增
D.2019年我国居民每月消费价格3月份较2月份有所下降
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,
,![]() 为过焦点
为过焦点![]() 且垂直于
且垂直于![]() 轴的抛物线
轴的抛物线![]() 的弦,已知以
的弦,已知以![]() 为直径的圆经过点
为直径的圆经过点![]() .
.
(1)求![]() 的值及该圆的方程;
的值及该圆的方程;
(2)设![]() 为
为![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 的切线,切点为
的切线,切点为![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=axlnx﹣x2﹣ax+1(a∈R)在定义域内有两个不同的极值点.
(1)求实数a的取值范围;
(2)设两个极值点分别为x1,x2,x1<x2,证明:f(x1)+f(x2)<2﹣x12+x22.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了贯彻落实党中央对新冠肺炎疫情防控工作的部署和要求,坚决防范疫情向校园蔓延,切实保障广大师生身体健康和生命的安全,教育主管部门决定通过电视频道、网络平台等多种方式实施线上教育教学工作.为了了解学生和家长对网课授课方式的满意度,从经济不发达的A城市和经济发达的B城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如下:
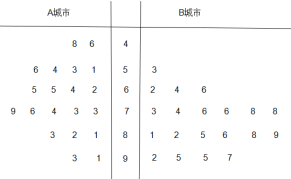
若评分不低于80分,则认为该用户对此授课方式“认可”,否则认为该用户对此授课方式“不认可”.以该样本中A,B城市的用户对此授课方式“认可”的频率分别作为A,B城市用户对此授课方式“认可”的概率.现从A城市和B城市的所有用户中分别随机抽取2个用户,用![]() 表示这4个用户中对此授课方式“认可”的用户个数,则
表示这4个用户中对此授课方式“认可”的用户个数,则![]() __________;用
__________;用![]() 表示从A城市随机抽取2个用户中对此授课方式“认可”的用户个数,则
表示从A城市随机抽取2个用户中对此授课方式“认可”的用户个数,则![]() 的数学期望为_________ .
的数学期望为_________ .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 中前两项
中前两项![]() 给定,若对于每个正整数
给定,若对于每个正整数![]() ,均存在正整数
,均存在正整数![]() (
(![]() )使得
)使得![]() ,则称数列
,则称数列![]() 为“
为“![]() 数列”.
数列”.
(1)若数列![]() 为
为![]() 的等比数列,当
的等比数列,当![]() 时,试问:
时,试问:![]() 与
与![]() 是否相等,并说明数列
是否相等,并说明数列![]() 是否为“
是否为“![]() 数列”;
数列”;
(2)讨论首项为![]() 、公差为
、公差为![]() 的等差数列
的等差数列![]() 是否为“
是否为“![]() 数列”,并说明理由;
数列”,并说明理由;
(3)已知数列![]() 为“
为“![]() 数列”,且
数列”,且![]() ,记
,记![]() ,
,![]() ,其中正整数
,其中正整数![]() , 对于每个正整数
, 对于每个正整数![]() ,当正整数
,当正整数![]() 分别取1、2、
分别取1、2、![]() 、
、![]() 时
时![]() 的最大值记为
的最大值记为![]() 、最小值记为
、最小值记为![]() . 设
. 设![]() ,当正整数
,当正整数![]() 满足
满足![]() 时,比较
时,比较![]() 与
与![]() 的大小,并求出
的大小,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com