
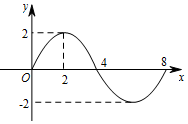
 函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象如示,则f(1)+f(2)+f(3)+…+f(210)的值等于( )
函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象如示,则f(1)+f(2)+f(3)+…+f(210)的值等于( )| A. | $\sqrt{2}$ | B. | $2+2\sqrt{2}$ | C. | $2+\sqrt{2}$ | D. | 0 |
分析 由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式,再利用三角函数的周期性,求得所给式子的值.
解答 解:根据函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象,
可得A=2,$\frac{1}{2}•\frac{2π}{ω}$=8-4,∴ω=$\frac{π}{4}$,
∴函数的解析式为y=2sin($\frac{π}{4}$x+φ),
再根据五点法作图可得$\frac{π}{4}•0$+φ=0,∴函数的解析式为y=2sin$\frac{π}{4}$x,
故函数的周期为$\frac{2π}{\frac{π}{4}}$=8,
f(1)+f(2)+f(3)+…+f(8)=$\sqrt{2}$+2+$\sqrt{2}$+0+(-$\sqrt{2}$)+(-2)+(-$\sqrt{2}$)+0=0,
∴f(1)+f(2)+f(3)+…+f(210)=f(1)+f(2)+f(3)+…+f(1024)
=128•[f(1)+f(2)+f(3)+…+f(8)]=0,
故选:D.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,三角函数的周期性的应用,属于中档题.


 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
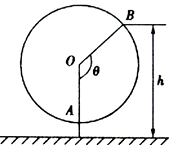 如图是一个缆车示意图,该缆车的半径为4.8m,圆上最低点与地面的距离为0.8m,缆车每60s转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面的距离为hm.
如图是一个缆车示意图,该缆车的半径为4.8m,圆上最低点与地面的距离为0.8m,缆车每60s转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面的距离为hm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com