练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图所示，在正四棱柱ABCD－A1B1C1D1中，E，F，G，H分别是CC1，C1D1，D1D，DC的中点，N是BC的中点，点M在四边形EFGH上或其内部运动，且使MN⊥AC.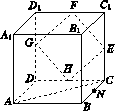

    对于下列命题：①点M可以与点H重合；②点M可以与点F重合；③点M可以在线段FH上；④点M可以与点E重合．其中真命题的序号是________(把真命题的序号都填上)．

    ①②③

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    已知PA垂直于正方形ABCD所在平面,连接PB、PC、PD、AC、BD,则下列垂直关系中正确的序号是              .

    ①平面平面PBC ②平面平面PAD ③平面平面PCD

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    如果点P在z轴上，且满足｜PO｜＝1（O是坐标原点），则点P到点A（1，1，1）的距离是   .

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    设α和β为不重合的两个平面,给出下列命题:
    ①若α内的两条相交直线分别平行于β内的两条直线,则α平行于β;
    ②若α外一条直线l与α内的一条直线平行,则l和α平行;
    ③设α和β相交于直线l,若α内有一条直线垂直于l,则α和β垂直;
    ④直线l与α垂直的充分必要条件是l与α内的两条直线垂直.
    上面命题中,真命题的序号是　　　　(写出所有真命题的序号). 

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    已知直线l⊥平面α,直线m?平面β,给出下列命题:①α∥β⇒l⊥m.②α⊥β⇒l∥m.③l∥m⇒α⊥β.④l⊥m⇒α∥β,其中正确命题的序号是　　　　.

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    在正方体ABCD ­A1B1C1D1中，点M，N分别在AB1，BC1上(M，N不与B1，C1重合)，且AM＝BN，那么①AA1⊥MN；②A1C1∥MN；③MN∥平面A1B1C1D1；④MN与A1C1异面，以上4个结论中，正确结论的序号是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    已知直线l⊥平面α，直线m?平面β，给出下列命题：
    ①α∥β⇒l⊥m；②α⊥β⇒l∥m；③l∥m⇒α⊥β；④l⊥m⇒α∥β.
    其中正确命题的序号是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    如图，AB与CD相交于点E，过E作BC的平行线与AD的延长线交于点P，已知∠A＝∠C，PD＝2DA＝2，则PE＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    下列四个正方体中，A，B为正方体的两个顶点，M，N，P分别为其所在棱的中点，能得出直线AB∥平面MNP的图形的序号是________(写出所有符合要求的图形序号)．

    查看答案和解析>>

    同步练习册答案