练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

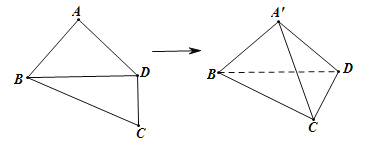
    【题目】（多选题）如图所示，在四边形中，，，.将四边形沿对角线折成四面体，使平面平面，则下列结论错误的结论是（ ）

    A.B.

    C.与平面所成的角为30°D.四面体的体积为

    【答案】ACD

    【解析】

    用反证法证明A错误.用勾股定理证得B正确.求得与平面所成的角，由此判断C错误.求得四面体的体积由此判断D错误.

    依题意可知，三角形是等腰直角三角形.由于平面平面，平面平面，，所以平面，则.

    对于A选项，假设，而，所以平面，则，这与矛盾，所以A选项错误.

    对于B选项，在三角形中，

    ，所以，所以，故B选项正确.

    对于C选项，由于平面，所以是与平面所成的角.由上述分析可知，三角形是等腰直角三角形，所以，故C选项错误.

    对于D选项，，故D选项错误.

    故选：ACD

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知圆，直线，.

    （1）证明：不论取任何实数，直线与圆恒交于两点；

    （2）当直线被圆截得的弦长最短时，求此最短弦长及直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数，

    （1）设函数的定义域为A

    ①若，，，求实数c的值.

    ②若，，，求M的最小值

    （2）若，对任意的，存在，使得不等式成立，求实数n的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知某圆的极坐标方程为，求

    (1)圆的普通方程和参数方程；

    (2)圆上所有点中的最大值和最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线的参数方程为（为参数）.以坐标原点为极点，以轴正半轴为极轴建立极坐标系，曲线的极坐标方程为.

    （1）求曲线的普通方程与曲线的直角坐标方程；

    （2）若与交于、两点，点的极坐标为，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2018年9月24日，阿贝尔奖和菲尔兹奖双料得主、英国著名数学家阿蒂亚爵士宣布自己证明了黎曼猜想，这一事件引起了数学届的震动。在1859年的时候，德国数学家黎曼向科学院提交了题目为《论小于某值的素数个数》的论文并提出了一个命题，也就是著名的黎曼猜想。在此之前，著名数学家欧拉也曾研究过这个问题，并得到小于数字的素数个数大约可以表示为的结论。若根据欧拉得出的结论，估计1000以内的素数的个数为_________(素数即质数，，计算结果取整数)

    A. 768 B. 144 C. 767 D. 145

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，函数，.

    （1）求的单调区间

    （2）讨论零点的个数

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某商场举行优惠促销活动，顾客仅可以从以下两种优惠方案中选择一种，

    方案一：每满200元减50元；

    方案二：每满200元可抽奖一次．具体规则是依次从装有3个红球、l个白球的甲箱，装有2个红球、2个白球的乙箱，以及装有1个红球、3个白球的丙箱中各随机摸出1个球，所得结果和享受的优惠如下表：（注：所有小球仅颜色有区别）

    红球个数

    3

    2

    1

    0

    实际付款

    半价

    7折

    8折

    原价

    （1）若两个顾客都选择方案二，各抽奖一次，求至少一个人获得半价优惠的概率；

    （2）若某顾客购物金额为320元，用所学概率知识比较哪一种方案更划算？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】李明自主创业，在网上经营一家水果店，销售的水果中有草莓、京白梨、西瓜、桃，价格依次为60元/盒、65元/盒、80元/盒、90元/盒．为增加销量，李明对这四种水果进行促销：一次购买水果的总价达到120元，顾客就少付x元．每笔订单顾客网上支付成功后，李明会得到支付款的80%．

    ①当x=10时，顾客一次购买草莓和西瓜各1盒，需要支付__________元；

    ②在促销活动中，为保证李明每笔订单得到的金额均不低于促销前总价的七折，则x的最大值为__________．

    查看答案和解析>>

    同步练习册答案