
在平面直角坐标系中,对于任意相邻三点都不共线的有序整点列(整点即横纵坐标都是整数的点)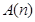 :
: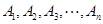 与
与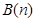 :
: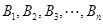 ,其中
,其中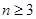 ,若同时满足:①两点列的起点和终点分别相同;②线段
,若同时满足:①两点列的起点和终点分别相同;②线段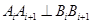 ,其中
,其中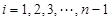 ,则称
,则称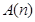 与
与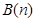 互为正交点列.
互为正交点列.
(1)求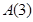 :
: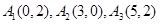 的正交点列
的正交点列 ;
;
(2)判断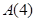 :
: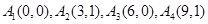 是否存在正交点列
是否存在正交点列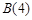 ?并说明理由;
?并说明理由;
(3)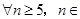 N,是否都存在无正交点列的有序整点列
N,是否都存在无正交点列的有序整点列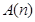 ?并证明你的结论.
?并证明你的结论.
(1)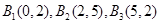 ,(2)不存在,(3)存在.
,(2)不存在,(3)存在.
解析试题分析:(1)因为 与
与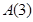 的起点和终点分别相同,所以
的起点和终点分别相同,所以 ,只需求
,只需求 .由
.由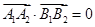 及
及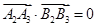 ,可解得
,可解得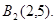 本题实质考查对新定义的理解.关键逐条代入验证.(2)与(1)相似,从求
本题实质考查对新定义的理解.关键逐条代入验证.(2)与(1)相似,从求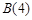 角度出发,能求出来就存在,否则就不存在.首先有
角度出发,能求出来就存在,否则就不存在.首先有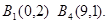 求
求 时,不是设四个未知数,二是利用向量垂直关系,设三个未知数,即
时,不是设四个未知数,二是利用向量垂直关系,设三个未知数,即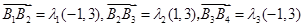 ,因为
,因为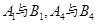 相同,所以有
相同,所以有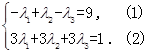 因为
因为
 ,所以方程组显然不成立,即不存在.
,所以方程组显然不成立,即不存在.
(3)按照(1)的思路,要保证方程组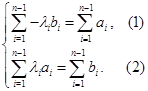 无解,须使得整数尽量取
无解,须使得整数尽量取 ,①当
,①当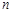 为偶数时,取
为偶数时,取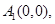
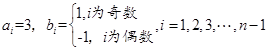 .②当
.②当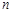 为奇数时,取
为奇数时,取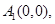
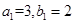 ,
,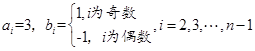 ,就可满足题意.
,就可满足题意.
试题解析:解:
(1)设点列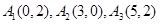 的正交点列是
的正交点列是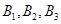 ,
,
由正交点列的定义可知 ,设
,设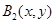 ,
,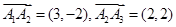 ,
,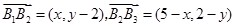 ,
,
由正交点列的定义可知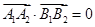 ,
,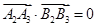 ,
,
即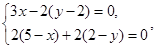 解得
解得
所以点列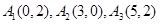 的正交点列是
的正交点列是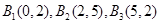 . 3分
. 3分
(2)由题可得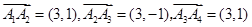 ,
,
设点列 是点列
是点列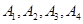 的正交点列,
的正交点列,
则可设 ,
,

因为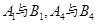 相同,所以有
相同,所以有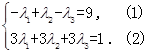
因为
 ,方程(2)显然不成立,
,方程(2)显然不成立,
所以有序整点列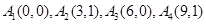 不存在正交点列; 8分
不存在正交点列; 8分
(3)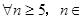
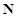 ,都存在整点列
,都存在整点列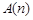 无正交点列. 9分
无正交点列. 9分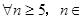
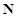 ,设
,设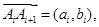 其中
其中 是一对互质整数,
是一对互质整数,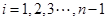
若有序整点列 是点列
是点列 正交点列,
正交点列,
则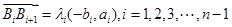 ,
,
则有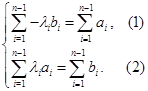
①当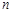 为偶数时,取
为偶数时,取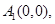
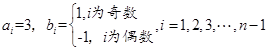 .
.
由于 是整点列,所以有
是整点列,所以有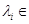
 ,
, .
.
等式(2)中左边是3的倍数,右边等于1,等式不成立,
所以该点列 无正交点列;
无正交点列;
②当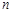 为奇数时,
为奇数时,
取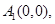


 名校课堂系列答案
名校课堂系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com