
【题目】设椭圆E的方程为![]() (a>b>0),点O为坐标原点,点A的坐标为(a,0),点B的坐标为(0,b),点M在线段AB上,满足BM=2MA,直线OM的斜率为
(a>b>0),点O为坐标原点,点A的坐标为(a,0),点B的坐标为(0,b),点M在线段AB上,满足BM=2MA,直线OM的斜率为![]() .
.
(1)求E的离心率e;
(2)设点C的坐标为(0,-b),N为线段AC的中点,点N关于直线AB的对称点的纵坐标为![]() ,求E的方程.
,求E的方程.
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】已知命题p:x∈R,2mx2+mx-![]() <0,命题q:2m+1>1.若“p∧q”为假,“p∨q”为真,则实数m的取值范围是( )
<0,命题q:2m+1>1.若“p∧q”为假,“p∨q”为真,则实数m的取值范围是( )
A. (-3,-1)∪[0,+∞) B. (-3,-1]∪[0,+∞)
C. (-3,-1)∪(0,+∞) D. (-3,-1]∪(0,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点A,B的坐标分别为(-2,0),(2,0)直线AM,BM相交于点M,且它们的斜率之积是-![]() .
.
(1)求点M的轨迹E的方程;
(2)设直线l:y=kx与E交于C,D两点,F1(-1,0),F2(1,0),若E上存在点P,使得![]() ,求实数k的取值范围.
,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
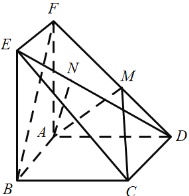
【题目】如图所示的几何体中,![]() 平面ABCD,四边形ABCD为菱形,
平面ABCD,四边形ABCD为菱形,![]() ,点M,N分别在棱FD,ED上.
,点M,N分别在棱FD,ED上.
(1)若![]() 平面MAC,设
平面MAC,设![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,平面AEN平面EDC所成的锐二面角为
,平面AEN平面EDC所成的锐二面角为![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 是以
是以![]() 为直径的圆上两点,
为直径的圆上两点,![]() ,
,![]() ,
,![]() 是
是![]() 上一点,且
上一点,且![]() ,将圆沿直径
,将圆沿直径![]() 折起,使点
折起,使点![]() 在平面
在平面![]() 的射影
的射影![]() 在
在![]() 上,已知
上,已知![]() .
.

(1)求证:![]() ⊥平面
⊥平面![]() ;
;
(2)求证:![]()
![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2014·江苏卷)如图,在平面直角坐标系xOy中,F1,F2分别是椭圆![]() (a>b>0)的左、右焦点,顶点B的坐标为(0,b),连接BF2并延长交椭圆于点A,过点A作x轴的垂线交椭圆于另一点C,连接F1C.
(a>b>0)的左、右焦点,顶点B的坐标为(0,b),连接BF2并延长交椭圆于点A,过点A作x轴的垂线交椭圆于另一点C,连接F1C.

(1)若点C的坐标为![]() ,且BF2=
,且BF2=![]() ,求椭圆的方程;
,求椭圆的方程;
(2)若F1C⊥AB,求椭圆离心率e的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店销售某海鲜,统计了春节前后50天该海鲜的需求量![]() (
(![]() ,单位:公斤),其频率分布直方图如图所示,该海鲜每天进货1次,商店每销售1公斤可获利50元;若供大于求,剩余的削价处理,每处理1公斤亏损10元;若供不应求,可从其它商店调拨,销售1公斤可获利30元.假设商店每天该海鲜的进货量为14公斤,商店的日利润为
,单位:公斤),其频率分布直方图如图所示,该海鲜每天进货1次,商店每销售1公斤可获利50元;若供大于求,剩余的削价处理,每处理1公斤亏损10元;若供不应求,可从其它商店调拨,销售1公斤可获利30元.假设商店每天该海鲜的进货量为14公斤,商店的日利润为![]() 元.
元.

(1)求商店日利润![]() 关于需求量
关于需求量![]() 的函数表达式;
的函数表达式;
(2)假设同组中的每个数据用该组区间的中点值代替.
①求这50天商店销售该海鲜日利润的平均数;
②估计日利润在区间![]() 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com