
【题目】设椭圆![]() ,定义椭圆
,定义椭圆![]() 的“相关圆
的“相关圆![]() ”的方程为
”的方程为![]() ,若抛物线
,若抛物线![]() 的焦点与椭圆
的焦点与椭圆![]() 的一个焦点重合,且椭圆
的一个焦点重合,且椭圆![]() 短轴的一个端点和其两个焦点构成直角三角形.
短轴的一个端点和其两个焦点构成直角三角形.
(1)求椭圆![]() 的方程和“相关圆
的方程和“相关圆![]() ”的方程;
”的方程;
(2)若直线![]() 与圆
与圆![]() 相切,且与椭圆
相切,且与椭圆![]() 交于
交于![]() 两点,
两点,![]() 为坐标原点.
为坐标原点.
①求证:![]() ;
;
②求![]() 的最大值.
的最大值.
【答案】(1)![]() ;
;![]() (2)①证明见解析; ②
(2)①证明见解析; ②![]()
【解析】
(1)由抛物线焦点为![]() 及椭圆
及椭圆![]() 短轴的一个端点和其两个焦点构成直角三角形,即可求得
短轴的一个端点和其两个焦点构成直角三角形,即可求得![]() ,从而可得到本题答案;
,从而可得到本题答案;
(2)①分直线l的斜率存在和不存在两种情况考虑,求出![]() 的值,即可得到本题结论;②算出直线斜率不存在时
的值,即可得到本题结论;②算出直线斜率不存在时![]() 的值,以及斜率存在时
的值,以及斜率存在时![]() 的最大值,通过比较大小,即可得到本题答案.
的最大值,通过比较大小,即可得到本题答案.
(1)易知抛物线焦点为![]() ,
,
又由![]() 的一个短轴端点与两焦点构成直角三角形,
的一个短轴端点与两焦点构成直角三角形,
可得![]() ,
,
![]() 椭圆
椭圆![]() 的方程为
的方程为![]() ,
,
相关圆![]() 的方程为
的方程为![]() .
.
(2)①(i)![]() 斜率不存在时,可得
斜率不存在时,可得![]() 的方程为
的方程为![]() ,
,
联立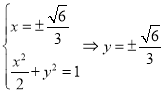 ,
,
即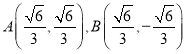 或
或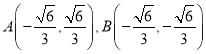
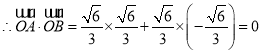 ,
,
![]() ;
;
(ii)斜率存在时,可设![]() 的方程为
的方程为![]() ,
,![]() ,联立
,联立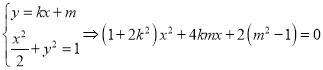 ,
,
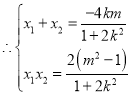 ,
,
由圆![]() 与
与![]() 相切可得
相切可得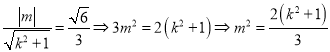 ,
,
![]()
![]()
![]()
![]() ,
,
![]() 由(i)(ii)知,
由(i)(ii)知,![]() 恒成立.
恒成立.
②![]() 斜率不存在时,由①可得
斜率不存在时,由①可得![]() ,
,
![]() 斜率存在时,由①可得
斜率存在时,由①可得
![]()
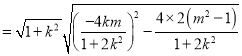
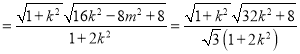 ,
,
令![]() ,则
,则![]() ,
,
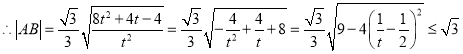 ,
,
(当且仅当![]() 时取“
时取“![]() ”)
”)
![]() .
.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:
【题目】我国在贵州省平塘县境内修建的500米口径球面射电望远镜(FAST)是目前世界上最大单口径射电望远镜.使用三年来,已发现132颗优质的脉冲星候选体,其中有93颗已被确认为新发现的脉冲星,脉冲星是上世纪60年代天文学的四大发现之一,脉冲星就是正在快速自转的中子星,每一颗脉冲星每两脉冲间隔时间(脉冲星的自转周期)是-定的,最小小到0.0014秒,最长的也不过11.765735秒.某-天文研究机构观测并统计了93颗已被确认为新发现的脉冲星的自转周期,绘制了如图的频率分布直方图.

(1)在93颗新发现的脉冲星中,自转周期在2至10秒的大约有多少颗?
(2)根据频率分布直方图,求新发现脉冲星自转周期的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年初,湖北出现由新型冠状病毒引发的肺炎.为防止病毒蔓延,各级政府相继启动重大突发公共卫生事件一级响应,全国人心抗击疫情.下图表示
年初,湖北出现由新型冠状病毒引发的肺炎.为防止病毒蔓延,各级政府相继启动重大突发公共卫生事件一级响应,全国人心抗击疫情.下图表示![]() 月
月![]() 日至
日至![]() 月
月![]() 日我国新型冠状病毒肺炎单日新增治愈和新增确诊病例数,则下列中表述错误的是( )
日我国新型冠状病毒肺炎单日新增治愈和新增确诊病例数,则下列中表述错误的是( )

A.![]() 月下旬新增确诊人数呈波动下降趋势
月下旬新增确诊人数呈波动下降趋势
B.随着全国医疗救治力度逐渐加大,![]() 月下旬单日治愈人数超过确诊人数
月下旬单日治愈人数超过确诊人数
C.![]() 月
月![]() 日至
日至![]() 月
月![]() 日新增确诊人数波动最大
日新增确诊人数波动最大
D.我国新型冠状病毒肺炎累计确诊人数在![]() 月
月![]() 日左右达到峰值
日左右达到峰值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有编号分别为1,2,3,4,5,6,7,8的八个小球和编号为1,2,3,4,5,6,7,8的八个盒子.现将这八个小球随机放入八个盒子内,要求每个盒子内放一个球,要求编号为偶数的小球在编号为偶数的盒子内,且至少有四个小球在相同编号的盒子内,则一共有______种投放方法.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com