
【题目】设函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 有两个极值点
有两个极值点![]() 和
和![]() ,记过点
,记过点![]() ,
,![]() 的直线的斜率为
的直线的斜率为![]() ,问:是否存在
,问:是否存在![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)见解析;(2)不存在
【解析】分析:(1)求得导函数![]() ,判断二次方程
,判断二次方程![]() 的根的情况得出
的根的情况得出![]() =0的解及
=0的解及![]() 在
在![]() 上的正负值变化,从而得单调性;
上的正负值变化,从而得单调性;
(2)假设存在,由(1)知![]() ,先表示出
,先表示出![]() 化简为
化简为![]() ,从而
,从而![]() ,再由
,再由![]() 消元,
消元,![]() (
(![]() ),设出新函数,通过导数研究出此方程无解,因此得不存在.
),设出新函数,通过导数研究出此方程无解,因此得不存在.
详解: (1)f(x)的定义域为(0,+∞),f′(x)=1+![]() -
-![]() =
=![]() .
.
令g(x)=x2-ax+1,则方程x2-ax+1=0的判别式Δ=a2-4.
①当|a|≤2时,Δ≤0,f′(x)≥0,故f(x)在(0,+∞)上单调递增.
②当a<-2时,Δ>0,g(x)=0的两根都小于0,在(0,+∞)上恒有f′(x)>0,
故f(x)在(0,+∞)上单调递增.
③当a>2时,Δ>0,g(x)=0的两根为x1=![]() ,x2=
,x2=![]() ,
,
当0<x<x1时,f′(x)>0;当x1<x<x2时,f′(x)<0;当x>x2时,f′(x)>0,
故f(x)在(0,x1),(x2,+∞)上单调递增,在(x1,x2)上单调递减.
(2)由(1)知,a>2.
因为f(x1)-f(x2)=(x1-x2)+![]() -a(ln x1-ln x2),
-a(ln x1-ln x2),
所以k=![]() =1+
=1+![]() -a·
-a·![]() .
.
又由(1)知,x1x2=1.于是k=2-a·![]() .
.
若存在a,使得k=2-a.则![]() =1.
=1.
即ln x1-ln x2=x1-x2.
亦即x2-![]() -2ln x2=0(x2>1). (*)
-2ln x2=0(x2>1). (*)
再由(1)知,函数h(t)=t-![]() -2ln t在(0,+∞)上单调递增,而x2>1,
-2ln t在(0,+∞)上单调递增,而x2>1,
所以x2-![]() -2ln x2>1-
-2ln x2>1-![]() -2ln 1=0.这与(*)式矛盾.
-2ln 1=0.这与(*)式矛盾.
故不存在a,使得k=2-a.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,![]() ,第五组,右图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )
,第五组,右图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )

A. 6 B. 8 C. 12 D. 18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,以坐标原点
为极点,以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,取相同的长度单位建立极坐标系,曲线
轴的非负半轴为极轴,取相同的长度单位建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若曲线![]() 上的点到直线
上的点到直线![]() 的最大距离为6,求实数
的最大距离为6,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABCD为直角梯形,∠C=∠CDA=90°,AD=2BC=2CD=2,P为平面ABCD外一点,且PB⊥BD.
(1)求证:PA⊥BD;
(2)若直线l过点P,且直线l∥直线BC,试在直线l上找一点E,使得直线PC∥平面EBD;
(3)若PC⊥CD,PB=4,求四棱锥P﹣ABCD的体积.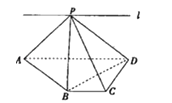
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C方程:![]() +
+![]() =1(a>b>0),M(x0 , y0)是椭圆C上任意一点,F(c,0)是椭圆的右焦点.
=1(a>b>0),M(x0 , y0)是椭圆C上任意一点,F(c,0)是椭圆的右焦点.
(1)若椭圆的离心率为e,证明|MF|=a﹣ex0;
(2)已知不过焦点F的直线l与圆x2+y2=b2相切于点Q,并与椭圆C交于A,B两点,且A,B两点都在y轴的右侧,若a=2,求△ABF的周长.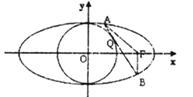
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】世界那么大,我想去看看,处在具有时尚文化代表的大学生们旅游动机强烈,旅游可支配收入日益增多,可见大学生旅游是一个巨大的市场.为了解大学生每年旅游消费支出(单位:百元)的情况,相关部门随机抽取了某大学的![]() 名学生进行问卷调查,并把所得数据列成如下所示的频数分布表:
名学生进行问卷调查,并把所得数据列成如下所示的频数分布表:
组别 |
|
|
|
|
|
频数 |
|
|
|
|
|
(Ⅰ)求所得样本的中位数(精确到百元);
(Ⅱ)根据样本数据,可近似地认为学生的旅游费用支出![]() 服从正态分布
服从正态分布![]() ,若该所大学共有学生
,若该所大学共有学生![]() 人,试估计有多少位同学旅游费用支出在
人,试估计有多少位同学旅游费用支出在![]() 元以上;
元以上;
(Ⅲ)已知样本数据中旅游费用支出在![]() 范围内的
范围内的![]() 名学生中有
名学生中有![]() 名女生,
名女生, ![]() 名男生,现想选其中
名男生,现想选其中![]() 名学生回访,记选出的男生人数为
名学生回访,记选出的男生人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:若![]() ,则
,则![]() ,
,
![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)
(1)应收集多少位女生样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为:![]() .估计该校学生每周平均体育运动时间超过4个小时的概率.
.估计该校学生每周平均体育运动时间超过4个小时的概率.

(3)在样本数据中,有60位女生的每周平均体育运动时间超过4个小时.请完成每周平均体育运动时间与性别的列联表,并判断是否有![]() 的把握认为“该校学生的每周平均体育运动时间与性别有关”.
的把握认为“该校学生的每周平均体育运动时间与性别有关”.
附:
![]()
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某住宅小区的平面图呈圆心角![]() 为的扇形
为的扇形![]() ,小区的两个出入口设置在点
,小区的两个出入口设置在点![]() 及点
及点![]() 处,且小区里有一条平行于
处,且小区里有一条平行于![]() 的小路
的小路![]() 。
。

(1)已知某人从![]() 沿
沿![]() 走到
走到![]() 用了
用了![]() 分钟,从
分钟,从![]() 沿
沿![]() 走到
走到![]() 用了
用了![]() 分钟,若此人步行的速度为每分钟
分钟,若此人步行的速度为每分钟![]() 米,求该扇形的半径
米,求该扇形的半径![]() 的长(精确到
的长(精确到![]() 米)
米)
(2)若该扇形的半径为![]() ,已知某老人散步,从
,已知某老人散步,从![]() 沿
沿![]() 走到
走到![]() ,再从
,再从![]() 沿
沿![]() 走到
走到![]() ,试确定
,试确定![]() 的位置,使老人散步路线最长。
的位置,使老人散步路线最长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com