
设函数f(x)是定义在[-1,0)∪(0,1]上的偶函数,当x∈[-1,0)时,f(x)=x3-ax(a∈R).
(1)当x∈(0,1]时,求f(x)的解析式;
(2)若a>3,试判断f(x)在(0,1]上的单调性,并证明你的结论;
(3)是否存在a,使得当x∈(0,1]时,f(x)有最大值1.
|
解:(1)∵x∈(0,1]时,-x∈[-1,0), ∴f(-x)=(-x)3-a(-x)=ax-x3. 又f(x)为偶函数,∴f(-x)=f(x),即f(x)=ax-x3. (2) ∴-3x2≥-3. ∵a>3,∴-3x2+a>0.故f(x)在(0,1]上为增函数. (3)假设存在a,使得当x∈(0,1]时,f(x)有最大值1. ∴ 即a>0时,x=± ∴f(x)极大值=f( ∴a= 思路分析:此题具有较强的综合性,应注意知识之间的相互转化和相互联系. |
|
关于存在性问题,处理的方法可以先假设存在,再寻找所得的结论. |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
(08年唐山一中一模文)(12分) 设函数f(x)是定义在R上的减函数,满足f(x+y)=f(x)•f(y)且f(0)=1,数列{an}满足
a1=4,f(log3![]() f(-1-log3
f(-1-log3![]() =1 (n∈N*)
=1 (n∈N*)
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{nan}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数f(x)是定义在R上的偶函数,并在区间(-∞,0)内单调递增,f(2a2+a+1)<f(3a2-2a+1).求a的取值范围,并在该范围内求函数y=(![]() )
)![]() 的单调递减区间.
的单调递减区间.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练7练习卷(解析版) 题型:填空题
设函数f(x)是定义在R上的周期为2的偶函数,当x∈[0,1]时,f(x)=x+1,则f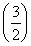 = .
= .
查看答案和解析>>
科目:高中数学 来源:2012届度河南泌阳二高高三第一次月考数学试卷 题型:填空题
设函数f(x) 是定义在R上的偶函数,且对任意的x ÎR恒有f(x+1)=-f(x),已知当x Î[0,1]时,f(x)=3x.则
① 2是f(x)的周期; ② 函数f(x)的最大值为1,最小值为0;
③ 函数f(x)在(2,3)上是增函数; ④ 直线x=2是函数f(x)图象的一条对称轴.
其中所有正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com