
| A. | 1 | B. | -$\frac{1}{2}$ | C. | 1或-$\frac{1}{2}$ | D. | -1或-$\frac{1}{2}$ |
分析 由题意存在实数k使λ$\overrightarrow{a}$+$\overrightarrow{b}$=k[$\overrightarrow{a}$+(2λ-1)$\overrightarrow{b}$],k<0,由向量$\overrightarrow{a}$,$\overrightarrow{b}$不共线,得2λ2-λ-1=0,由此能求出结果.
解答 解:∵向量$\overrightarrow{a}$,$\overrightarrow{b}$不共线,且向量$\overrightarrow{c}$=λ$\overrightarrow{a}$+$\overrightarrow{b}$,$\overrightarrow{d}$=$\overrightarrow{a}$+(2λ-1)$\overrightarrow{b}$,$\overrightarrow{c}$与$\overrightarrow{d}$反向,
∴存在实数k使$\overrightarrow{c}$=k$\overrightarrow{d}$(k<0),
于是λ$\overrightarrow{a}$+$\overrightarrow{b}$=k[$\overrightarrow{a}$+(2λ-1)$\overrightarrow{b}$].
整理得λ$\overrightarrow{a}$+$\overrightarrow{b}$=k$\overrightarrow{a}$+(2λk-k)$\overrightarrow{b}$.
由于向量$\overrightarrow{a}$,$\overrightarrow{b}$不共线,所以有$\left\{\begin{array}{l}{λ=k}\\{2λk-k=1}\end{array}\right.$,
整理得2λ2-λ-1=0,
解得λ=1或λ=-$\frac{1}{2}$.
又因为k<0,所以λ<0,
故λ=-$\frac{1}{2}$.
故选:B.
点评 本题考查实数值的求法,是中档题,解题时要认真审题,注意向量共线的性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
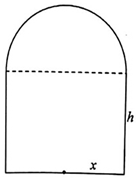 某制瓶厂要制造一批轴截面如图所示的瓶子,瓶子是按照统一规格设计的,瓶体上部为半球体,下部为圆柱体,并保持圆柱体的容积为3π.设圆柱体的底面半径为x,圆柱体的高为h,瓶体的表面积为S.
某制瓶厂要制造一批轴截面如图所示的瓶子,瓶子是按照统一规格设计的,瓶体上部为半球体,下部为圆柱体,并保持圆柱体的容积为3π.设圆柱体的底面半径为x,圆柱体的高为h,瓶体的表面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com