
【题目】在平面直角坐标系中,横、纵坐标均为整数的点叫做格点.若函数图象恰好经过k个格点,则称函数为k阶格点函数.已知函数:
①y=sinx; ②y=cos(x+![]() ); ③y=ex-1; ④y=x2.
); ③y=ex-1; ④y=x2.
其中为一阶格点函数的序号为 ( )
A. ①② B. ②③ C. ①③ D. ②④
【答案】C
【解析】对于①,注意到y=sinx的值域是[-1,1];当sinx=0时,x=kπ(k∈Z),此时相应的整数x=0;当sinx=±1时,x=kπ+![]() (k∈Z),此时没有相应的整数x,因此函数y=sinx仅过唯一的整点(0,0),该函数是一阶格点函数.同理可知,对于②,函数y=cos(x+
(k∈Z),此时没有相应的整数x,因此函数y=sinx仅过唯一的整点(0,0),该函数是一阶格点函数.同理可知,对于②,函数y=cos(x+![]() )不是一阶格点函数.对于③,令y=ex-1=k(k∈Z)得ex=k+1>0,x=ln(k+1),仅当k=0时,x=0∈Z,因此函数y=ex-1是一阶格点函数.对于④,注意到函数y=x2的图象经过多个整点,如点(0,0),(1,1),因此函数y=x2不是一阶格点函数.综上所述知选C.
)不是一阶格点函数.对于③,令y=ex-1=k(k∈Z)得ex=k+1>0,x=ln(k+1),仅当k=0时,x=0∈Z,因此函数y=ex-1是一阶格点函数.对于④,注意到函数y=x2的图象经过多个整点,如点(0,0),(1,1),因此函数y=x2不是一阶格点函数.综上所述知选C.


科目:高中数学 来源: 题型:
【题目】上半年产品产量与单位成本资料如下:
月份 | 产量/千件 | 单位成本/元 |
1 | 2 | 73 |
2 | 3 | 72 |
3 | 4 | 71 |
4 | 3 | 73 |
5 | 4 | 69 |
6 | 5 | 68 |
且已知产量x与单位成本y具有线性相关关系.
(1)求出回归方程.
(2)指出产量每增加1 000件时,单位成本平均变动多少?
(3)假定产量为6 000件时,单位成本为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为![]() 与
与![]() ,且乙投球3次均未命中的概率为
,且乙投球3次均未命中的概率为![]() ,甲投球未命中的概率恰是乙投球未命中的概率的2倍.
,甲投球未命中的概率恰是乙投球未命中的概率的2倍.
(Ⅰ)求乙投球的命中率![]() ;
;
(Ⅱ)若甲投球1次,乙投球2次,两人共命中的次数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x/元 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y/件 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求线性回归方程![]() =
=![]() x+
x+![]() ,其中
,其中![]() =-20,
=-20, ![]() =
=![]() -
-![]()
![]() .
.
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在调查运动员是否服用过兴奋剂的时候,给出两个问题作答,无关紧要的问题是:“你的身份证号码的尾数是奇数吗?”敏感的问题是:“你服用过兴奋剂吗?”然后要求被调查的运动员掷一枚硬币,如果出现正面,就回答第一个问题,否则回答第二个问题.由于回答哪一个问题只有被测试者自己知道,所以应答者一般乐意如实地回答问题.若我们把这种方法用于300个被调查的运动员,得到80个“是”的回答,则这群运动员中服用过兴奋剂的百分率大约为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 是棱
是棱![]() 上的点,
上的点, ![]() ,
, ![]() ,
, ![]() .
.
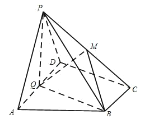
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 大小为
大小为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现从某班的一次期末考试中,随机的抽取了七位同学的数学(满分150分)、物理(满分110分)成绩如下表所示,数学、物理成绩分别用特征量![]() 表示,
表示,
特征量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
t | 101 | 124 | 119 | 106 | 122 | 118 | 115 |
y | 74 | 83 | 87 | 75 | 85 | 87 | 83 |
求![]() 关于t的回归方程;
关于t的回归方程;
(2)利用(1)中的回归方程,分析数学成绩的变化对物理成绩的影响,并估计该班某学生数学成绩130分时,他的物理成绩(精确到个位).
附:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
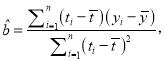
![]() .
. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com