某赛季,甲、乙两名篮球运动员都参加了7场比赛,他们所有比赛得分的情况如下:
甲:15,17,14,23,22,24,32;
乙:12,13,11,23,27,31,30.
(1)求甲、乙两名运动员得分的中位数.
(2)分别求甲、乙两名运动员得分的平均数、方差,你认为哪位运动员的成绩更稳定?
(3)如果从甲、乙两位运动员的7场得分中各随机抽取一场的得分,求甲的得分大于乙的得分的概率.(参考数据:92+82+102+22+62+102+92=466,72+42+62+32+12+22+112=236)
解:(1)将数据甲由大到小排列:32,24,23,22,17,15,14.甲运动员得分的中位数是22.同样的可知乙运动员得分的中位数是23
(2)

=

(14+17+15+24+22+23+32)=21.

=

(12+13+11+23+27+31+30)=21.
S
甲2=

[(21-14)
2+(21-17)
2+…+(21-32)
2]=
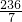
S
乙2=

[(21-12)
2+(21-13)
2+…(21-30)
2]=
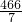
∴S
甲2<S
乙2∴甲运动员的成绩更稳定.
(3)从甲、乙两位运动员的7场得分中各随机抽取一场的得分的基本事件总数为49 (11分)
其中甲的得分大于乙的是:甲得14分有3场,甲得17分有3场,甲得15分有3场甲得24分有4场,甲得22分有3场,甲得23分有3场,甲得32分有7场,共计26场∴甲的得分大于乙的得分的概率 P=
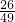
分析:(1)求中位数首先将数据由大到小或由小到大的顺序排列,取中间项的值或中间两项的算术平均数.
(2)利用平均数,方差公式计算,得出结论
(3)是古典概型.从甲、乙两位运动员的7场得分中各随机抽取一场共包括7×7=49种等可能行基本事件.逐一列举出甲的得分大于乙的得分所包含的基本事件个数.再利用公式计算即可.
点评:对于一组数据,通常要求的是这组数据的众数,中位数,平均数,方差等,体现数学的实用功能.

 =
= (14+17+15+24+22+23+32)=21.
(14+17+15+24+22+23+32)=21. =
= (12+13+11+23+27+31+30)=21.
(12+13+11+23+27+31+30)=21. [(21-14)2+(21-17)2+…+(21-32)2]=
[(21-14)2+(21-17)2+…+(21-32)2]=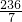 S乙2=
S乙2= [(21-12)2+(21-13)2+…(21-30)2]=
[(21-12)2+(21-13)2+…(21-30)2]=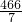
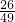


 字词句段篇系列答案
字词句段篇系列答案 某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们每场比赛得分的情况用如右图所示的茎叶图表示,则甲、乙两名运动员比赛得分的中位数分别是
某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们每场比赛得分的情况用如右图所示的茎叶图表示,则甲、乙两名运动员比赛得分的中位数分别是