
【题目】电视传媒公司为了了解某地区电视观众对某体育节目的收视情况,随机抽取了100名观众进行调查,下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.
(1)根据已知条件完成下面2×2列联表,并据此资料你是否认为“体育迷”与性别有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
(2)将上述调查所得到的频率视为概率.现在从该地区大量电视观众中,采用随机抽样方法每次抽取1名观众,抽取3次,记被抽取的3名观众中的“体育迷”人数为X,若每次抽取的结果是相互独立的,求X的分布列,期望E(X)和方差D(X)
P( K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |
【答案】
(1)解:由频率分布直方图可知,在抽取的100人中,“体育迷”有25人,从而2×2列联表如下:
非体育迷 | 体育迷 | 合计 | |
男 | 30 | 15 | 45 |
女 | 45 | 10 | 55 |
合计 | 75 | 25 | 100 |
将2×2列联表中的数据代入公式计算,得:
K2= ![]() =
= ![]() ≈3.03,
≈3.03,
因为3.03<3.841,所以没有理由认为“体育迷”与性别有关.
(2)解:由频率分布直方图知抽到“体育迷”的频率是0.25,将频率视为概率,即从观众中抽取到一名“体育迷”的概率是 ![]() ,
,
由题意X∽B(3, ![]() ),从而分布列为
),从而分布列为
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
所以E(X)=np=3× ![]() =
= ![]() .D(X)=npq=3×
.D(X)=npq=3× ![]() ×
× ![]() =
= ![]() .
.
【解析】(1)根据所给的频率分布直方图得出数据列出列联表,再代入公式计算得出K2 , 与3.841比较即可得出结论;(2)由题意,用频率代替概率可得出从观众中抽取到一名“体育迷”的概率是 ![]() ,由于X∽B(3,
,由于X∽B(3, ![]() ),从而给出分布列,再由公式计算出期望与方差即可
),从而给出分布列,再由公式计算出期望与方差即可
【考点精析】利用频率分布直方图对题目进行判断即可得到答案,需要熟知频率分布表频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为了解心肺疾病是否与年龄相关,现随机抽取80名市民,得到数据如下表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
大于40岁 | 16 | ||
小于或等于40岁 | 12 | ||
合计 | 80 |
已知在全部的80人中随机抽取1人,抽到不患心肺疾病的概率为 ![]()
下面的临界值表供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
(1)请将2×2列联表补充完整;
(2)能否在犯错误的概率不超过0.025的前提下认为患心肺疾病与年龄有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() :
: ![]() ,
, ![]() ,…,
,…, ![]() (
(![]() )中
)中![]() (
(![]() )且对任意的
)且对任意的![]()
![]() 恒成立,则称数列
恒成立,则称数列![]() 为“
为“![]() 数列”.
数列”.
(Ⅰ)若数列![]() ,
, ![]() ,
, ![]() ,
, ![]() 为“
为“![]() 数列”,写出所有可能的
数列”,写出所有可能的![]() ,
, ![]() ;
;
(Ⅱ)若“![]() 数列”
数列”![]() :
: ![]() ,
, ![]() ,…,
,…, ![]() 中,
中, ![]() ,
, ![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ)设![]() 为给定的偶数,对所有可能的“
为给定的偶数,对所有可能的“![]() 数列”
数列”![]() :
: ![]() ,
, ![]() ,…,
,…, ![]() ,
,
记![]() ,其中
,其中![]() 表示
表示![]() ,
, ![]() ,…,
,…, ![]() 这
这![]() 个数中最大的数,求
个数中最大的数,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在古希腊毕达哥拉斯学派把1,3,6,10,15,21,28,…这些数叫做三角形数,因为这些数对应的点可以排成一个正三角形则第n个三角形数为 . 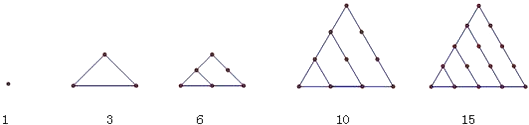
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知Rt△ABC,∠ABC=90°,D是AC的中点,⊙O经过A,B,D三点,CB的延长线交⊙O于点E,过点E作⊙O的切线,交AC的延长线于点F.在满足上述条件的情况下,当∠CAB的大小变化时,图形也随着改变,但在这个变化过程中,有些线段总保持着相等的关系.

(1)连接图中已标明字母的某两点,得到一条新线段与线段CE相等,并说明理由;
(2)若CF=CD,求sin F的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com