
【题目】命题p:α∈R,sin(π﹣α)=cosα;命题q:“0<a<4”是“关于x的不等式ax2+ax+1>0的解集是实数集R”的充分必要条件,则下面结论正确的是( )
A.p是假命题
B.q是真命题
C.“p∧q”是假命题
D.“p∨q”是假命题
【答案】C
【解析】解:sin(π﹣α)=sinα,当α= ![]() 时,sin(π﹣α)=sinα=cosα,
时,sin(π﹣α)=sinα=cosα,
故命题p是真命题;
要使不等式ax2+ax+1>0的解集为R,
①当a=0时,1>0恒成立,满足条件;
②当a≠0时,满足 ![]() ,解得0<a<4,
,解得0<a<4,
因此要不等式ax2+ax+1>0的解集为R,必有0≤a<4,
故“0<a<4”是“ax2+ax+1>0的解集是实数集R”的充分不必要条件,
故命题q是假命题;
故p∧q”是假命题;
故选:C.
【考点精析】关于本题考查的复合命题的真假,需要了解“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真才能得出正确答案.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 分别是双曲线E:
分别是双曲线E: ![]()
![]() 的左、右焦点,P是双曲线上一点,
的左、右焦点,P是双曲线上一点, ![]() 到左顶点的距离等于它到渐近线距离的2倍,(1)求双曲线的渐近线方程;(2)当
到左顶点的距离等于它到渐近线距离的2倍,(1)求双曲线的渐近线方程;(2)当![]() 时,
时, ![]() 的面积为
的面积为![]() ,求此双曲线的方程。
,求此双曲线的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在高二年级实行选课走班教学,学校为学生提供了多种课程,其中数学科提供5种不同层次的课程,分别称为数学1、数学2、数学3、数学4、数学5,每个学生只能从这5种数学课程中选择一种学习,该校高二年级1800名学生的数学选课人数统计如表:
课程 | 数学1 | 数学2 | 数学3 | 数学4 | 数学5 | 合计 |
选课人数 | 180 | 540 | 540 | 360 | 180 | 1800 |
为了了解数学成绩与学生选课情况之间的关系,用分层抽样的方法从这1800名学生中抽取了10人进行分析.
(1)从选出的10名学生中随机抽取3人,求这3人中至少有2人选择数学2的概率;
(2)从选出的10名学生中随机抽取3人,记这3人中选择数学2的人数为X,选择数学1的人数为Y,设随机变量ξ=X﹣Y,求随机变量ξ的分布列和数学期望E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
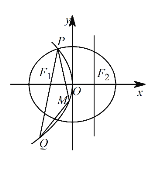
【题目】如图,设抛物线 ![]() :
:![]() 的准线
的准线 ![]() 与
与 ![]() 轴交于椭圆
轴交于椭圆 ![]() :
:![]() 的右焦点
的右焦点 ![]() ,
,![]() 为
为 ![]() 的左焦点.椭圆的离心率为
的左焦点.椭圆的离心率为 ![]() ,抛物线
,抛物线 ![]() 与椭圆
与椭圆 ![]() 交于
交于 ![]() 轴上方一点
轴上方一点 ![]() ,连接
,连接 ![]() 并延长交
并延长交 ![]() 于点
于点 ![]() ,
,![]() 为
为 ![]() 上一动点,且在
上一动点,且在 ![]() ,
,![]() 之间移动.
之间移动.
(1)当![]() 时,求
时,求 ![]() 的方程;
的方程;
(2)若 ![]() 的边长恰好是三个连续的自然数。求
的边长恰好是三个连续的自然数。求![]() 到直线
到直线![]() 距离的最大值以及此时
距离的最大值以及此时![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中内动点P(x,y)到圆F:x2+(y﹣1)2=1的圆心F的距离比它到直线y=﹣2的距离小1.
(1)求动点P的轨迹方程;
(2)设点P的轨迹为曲线E,过点F的直线l的斜率为k,直线l交曲线E于A,B两点,交圆F于C,D两点(A,C两点相邻).
①若 ![]() =t
=t ![]() ,当t∈[1,2]时,求k的取值范围;
,当t∈[1,2]时,求k的取值范围;
②过A,B两点分别作曲线E的切线l1 , l2 , 两切线交于点N,求△ACN与△BDN面积之积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:条件p:实数t满足使对数log2(﹣2t2+7t﹣5)有意义;条件q:实数t满足不等式t2﹣(a+3)t+a+2<0
(1)若命题¬p为真,求实数t的取值范围;
(2)若命题p是命题q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年上半年,股票投资人袁先生同时投资了甲、乙两只股票,其中甲股票赚钱的概率为 ![]() ,赔钱的概率是
,赔钱的概率是 ![]() ;乙股票赚钱的概率为
;乙股票赚钱的概率为 ![]() ,赔钱的概率为
,赔钱的概率为 ![]() .对于甲股票,若赚钱则会赚取5万元,若赔钱则损失4万元;对于乙股票,若赚钱则会赚取6万元,若赔钱则损失5万元.
.对于甲股票,若赚钱则会赚取5万元,若赔钱则损失4万元;对于乙股票,若赚钱则会赚取6万元,若赔钱则损失5万元.
(Ⅰ)求袁先生2016年上半年同时投资甲、乙两只股票赚钱的概率;
(Ⅱ)试求袁先生2016年上半年同事投资甲、乙两只股票的总收益的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣2)2+(y﹣3)2=16及直线l:(m+2)x+(3m+1)y=15m+10(m∈R).
(1)证明:不论m取什么实数,直线l与圆C恒相交;
(2)求直线l被圆C截得的弦长的最短长度及此时的直线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com