【题目】函数
的定义域为
，函数
.
（1）若
时，
的解集为
，求
；
（2）若存在
使得不等式
成立，求实数
的取值范围.
【答案】（1）
；（2）
.
【解析】
（1）求出集合A，B，由交集运算的定义，可得A∩B；
（2）若存在
使得不等式g（x）≤﹣1成立，即存在使得不等式﹣m
成立，得﹣m≥（
）min，解得实数m的取值范围．
（1）由x2+2x﹣8＞0，解得：x∈（﹣∞，﹣4）∪（2，+∞），
故则函数f（x）＝log3（x2+2x﹣8）的定义域A＝（﹣∞，﹣4）∪（2，+∞），
若m＝﹣4，g（x）＝x2﹣3x﹣4，由x2﹣3x﹣4≤0，解得：x∈[﹣1，4]，则B＝[﹣1，4]
所以A∩B＝（2，4]；
（2）存在使得不等式x2+（m+1）x+m≤﹣1成立，
即存在使得不等式﹣m成立，所以﹣m≥（）min
因为
x+1
1≥1，
当且仅当x+1＝1，即x＝0时取得等号
所以﹣m≥1，
解得：m≤﹣1．
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】下列说法中正确的是（ ）
A. “
”是“
”成立的充分不必要条件
B. 命题
，则
C. 为了了解800名学生对学校某项教改试验的意见，用系统抽样的方法从中抽取一个容量为40的样本，则分组的组距为40
D. 已知回归直线的斜率的估计值为1.23，样本点的中心为
，则回归直线方程为
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
和直线
： 
，椭圆的离心率
，坐标原点到直线
的距离为
.
（Ⅰ）求椭圆的方程；
（Ⅱ）已知定点
，若直线
过点
且与椭圆相交于
两点，试判断是否存在直线
，使以
为直径的圆过点
？若存在，求出直线
的方程；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某创业投资公司投资开发某种新能源产品，估计能获得10万元到100万元的投资收益，现准备制定一个对科研课题组的奖励方案：①奖金
（单位：万元）随投资收益
（单位：万元）的增加而增加；②奖金不超过9万元；③奖金不超过投资收益的20％.
（1）若建立函数
模型制定奖励方案，试用数学语言表述该公司对奖励函数
模型的基本要求，并分析函数
是否符合公司要求的奖励函数模型，并说明原因；
（2）若该公司采用模型函数
作为奖励函数模型，试确定最小的正整数
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如右图，一个直径为1的小圆沿着直径为2的大圆内壁的逆时针方
向滚动，M和N是小圆的一条固定直径的两个端点.那么，当小圆这
样滚过大圆内壁的一周，点M，N在大圆内所绘出的图形大致是( )
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图是某商场2018年洗衣机、电视机和电冰箱三种电器各季度销量的百分比堆积图（例如：第3季度内，洗衣机销量约占
，电视机销量约占
，电冰箱销量约占
）.根据该图，以下结论中一定正确的是（ ）
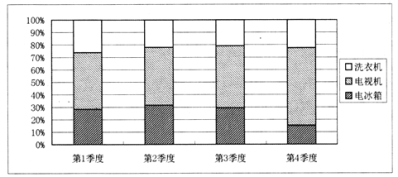
A. 电视机销量最大的是第4季度
B. 电冰箱销量最小的是第4季度
C. 电视机的全年销量最大
D. 电冰箱的全年销量最大
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】考虑下面两个定义域为（0，+∞）的函数f（x）的集合：
对任何不同的两个正数
，都有
，
=
对任何不同的两个正数，都有
（1）已知
，若
，且
，求实数
和
的取值范围
（2）已知
，且
的部分函数值由下表给出：
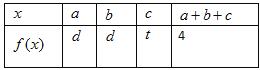
比较
与4的大小关系
（3）对于定义域为
的函数
，若存在常数
，使得不等式
对任何
都成立，则称为
的上界，将
中所有存在上界的函数组成的集合记作
，判断是否存在常数
，使得对任何
和
，都有
，若存在，求出的最小值，若不存在，说明理由
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设
为抛物线
的焦点，过点的直线
与抛物线
相交于
、
两点.
（1）若
，求此时直线的方程；
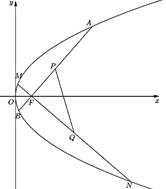
（2）若与直线垂直的直线
过点，且与抛物线相交于点
、
，设线段
、
的中点分别为
、
，如图，求证：直线
过定点；
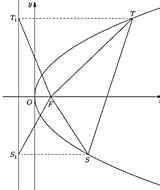
（3）设抛物线上的点
、
在其准线上的射影分别为
、
，若△
的面积是△
的面积的两倍，如图，求线段
中点的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
