
| x | (-∞,ln2) | ln2 | (ln2,+∞) |
| f ′(x) | - | 0 | + |
| f(x) | 单调递减↘ | 2(1-ln2+a) | 单调递增↗ |


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源:不详 题型:解答题
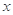 亿元,其中用于风景区改造为
亿元,其中用于风景区改造为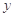 亿元。该市决定建立生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用
亿元。该市决定建立生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用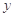 随每年改造生态环境总费用
随每年改造生态环境总费用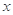 增加而增加;②每年改造生态环境总费用至少
增加而增加;②每年改造生态环境总费用至少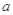 亿元,至多
亿元,至多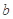 亿元;③每年用于风景区改造费用
亿元;③每年用于风景区改造费用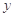 不得低于每年改造生态环境总费用
不得低于每年改造生态环境总费用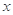 的15%,但不得高于每年改造生态环境总费用
的15%,但不得高于每年改造生态环境总费用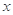 的25%.
的25%.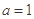 ,
,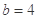 ,请你分析能否采用函数模型y=
,请你分析能否采用函数模型y=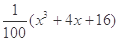 作为生态环境改造投资方案.
作为生态环境改造投资方案.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
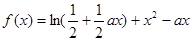 。(
。(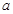 为常数,
为常数,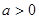 )
)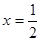 是函数
是函数 的一个极值点,求
的一个极值点,求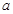 的值;
的值;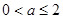 时,
时, 在
在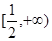 上是增函数;
上是增函数;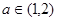 ,总存在
,总存在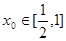 ,使不等式
,使不等式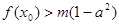 成立,求实数
成立,求实数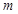 的取值范围。
的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,g(x)=x2-2ax+4,若任意x1∈[0,1],存在x2∈[1,2],使f(x1)≥g(x2),则实数a的取值范围是______.
,g(x)=x2-2ax+4,若任意x1∈[0,1],存在x2∈[1,2],使f(x1)≥g(x2),则实数a的取值范围是______.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com