
A、
| ||
B、
| ||
C、
| ||
D、
|
| 100 |
| 210 |
| 10 |
| 21 |


科目:高中数学 来源: 题型:
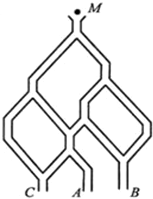 如图,一个小球从M处投入,通过管道自上而下落A或B或C.已知小球从每个叉口落入左右两个管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A,B,C,则分别设为l,2,3等奖.
如图,一个小球从M处投入,通过管道自上而下落A或B或C.已知小球从每个叉口落入左右两个管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A,B,C,则分别设为l,2,3等奖.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| d |
| d |
| OQ |
| 1 |
| 18 |
| 1 |
| 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010年上海市崇明县高考数学二模试卷(文科)(解析版) 题型:解答题
 ,圆C:(x-a)2+(y-b)2=r2的圆心为Q(a,b),半径为r.如果从{1,2,3,4,…,9,10}中任取3个不同的元素分别作为a,b,r的值,得到不同的圆,能够使得
,圆C:(x-a)2+(y-b)2=r2的圆心为Q(a,b),半径为r.如果从{1,2,3,4,…,9,10}中任取3个不同的元素分别作为a,b,r的值,得到不同的圆,能够使得 (O为坐标原点)的概率等于 .(用分数表示)
(O为坐标原点)的概率等于 .(用分数表示)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com