
【题目】设数列:A:a1,a2,…,an,B:b1,b2,…,bn.已知ai,bj∈{0,1}(i=1,2,…,n;j=1,2,…,n),定义n×n数表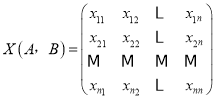 ,其中xij
,其中xij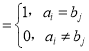 .
.
(1)若A:1,1,1,0,B:0,1,0,0,写出X(A,B);
(2)若A,B是不同的数列,求证:n×n数表X(A,B)满足“xij=xji(i=1,2,…,n;j=1,2,…,n;i![]() j)”的充分必要条件为“ak+bk=1(k=1,2,…,n)”;
j)”的充分必要条件为“ak+bk=1(k=1,2,…,n)”;
(3)若数列A与B中的1共有n个,求证:n×n数表X(A,B)中1的个数不大于![]() .
.
【答案】(1)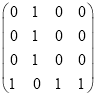 ;(2)证明见解析;(3)证明见解析.
;(2)证明见解析;(3)证明见解析.
【解析】
(1)根据题中给的定义写出X(A,B);
(2)可先证充分性,充分性由定义易证;再证必要性,注意分类讨论:先分a1=0和a1=1两类,a1=0较易证明,对a1=1再分b1=0和b1=1两类证明,运用xij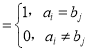 分析推理可得;
分析推理可得;
(3)根据数列A与B中的1共有n个,设A中1的个数为p,则A中0的个数为n﹣p,B中1的个数为n﹣p,B中0的个数为p.表示出n×n数表X(A,B)中1的个数,再用不等式证得n×n数表X(A,B)中1的个数不大于![]() .
.
(1)解: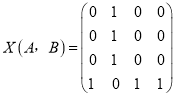 .
.
(2)证明:充分性
若ak+bk=1(k=1,2,…,n),由于xij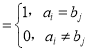 ,xji
,xji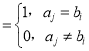 ,
,
令 A:a1,a2,…,an,由此数列 B:1﹣a1,1﹣a2,…,1﹣an.
由于 ai=bjai=1﹣ajai+aj=1aj=1﹣aiaj=bi.
从而有 xij=xji(i=1,2,…,n;j=1,2,…,n;i![]() j).
j).
必要性
若xij=xji(i=1,2,…,n;j=1,2,…,n;i![]() j).
j).
由于A,B是不同的数列,
设a1=1,b1=0,对任意的正整数k>1,
①若x1k=xk1=1,可得 a1=bk=1,ak=b1=0,
所以 ak+bk=1.
②若x1k=xk1=0,可得 bk=0,ak=1,
所以ak+bk=1.
同理可证 ![]() ,b1=1时,有ak+bk=1(k=1,2,…,n)成立.
,b1=1时,有ak+bk=1(k=1,2,…,n)成立.
设a1=1,b1=
①若x1k=xk1=1,可得a1=bk=1,ak=b1=1,
所以有ak=bk=1,则A,B是相同的数列,不符合要求.
②若x1k=xk1=0,可得bk=0,ak=0,
所以有ak=bk,则A,B是相同的数列,不符合要求.
同理可证 a1=0,b1=0时,A,B是相同的数列,不符合要求.
综上,有n×n数表X(A,B)满足“xij=xji”的充分必要条件为“ak+bk=1(k=1,2,…,n)”.
(3)证明:由于数列A,B中的1共有n个,设A中1的个数为p,
由此,A中0的个数为n﹣p,B中1的个数为n﹣p,B中0的个数为p.
若 ai=1,则数表X(A,B)的第i行为数列B:b1,b2,…,bn,
若 ai=0,则数表X(A,B)的第i行为数列B:1﹣b1,1﹣b2,…,1﹣bn,
所以 数表X(A,B)中1的个数为![]() .
.
所以 n×n数表X(A,B)中1的个数不大于![]() .
.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是矩形,A1D与AD1交于点E,AA1=AD=2AB=4.
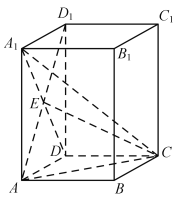
(1)证明:AE⊥平面ECD.
(2)求直线A1C与平面EAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
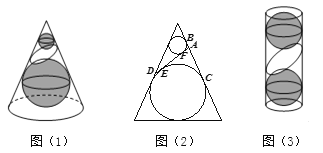
【题目】如图(1),在圆锥内放两个大小不同且不相切的球,使得它们分别与圆锥的侧面、底面相切,用与两球都相切的平面截圆锥的侧面得到截口曲线是椭圆.理由如下:如图(2),若两个球分别与截面相切于点![]() ,在得到的截口曲线上任取一点
,在得到的截口曲线上任取一点![]() ,过点
,过点![]() 作圆锥母线,分别与两球相切于点
作圆锥母线,分别与两球相切于点![]() ,由球与圆的几何性质,得
,由球与圆的几何性质,得![]() ,
,![]() ,所以
,所以![]() ,且
,且![]() ,由椭圆定义知截口曲线是椭圆,切点
,由椭圆定义知截口曲线是椭圆,切点![]() 为焦点.这个结论在圆柱中也适用,如图(3),在一个高为
为焦点.这个结论在圆柱中也适用,如图(3),在一个高为![]() ,底面半径为
,底面半径为![]() 的圆柱体内放球,球与圆柱底面及侧面均相切.若一个平面与两个球均相切,则此平面截圆柱所得的截口曲线也为一个椭圆,则该椭圆的离心率为______.
的圆柱体内放球,球与圆柱底面及侧面均相切.若一个平面与两个球均相切,则此平面截圆柱所得的截口曲线也为一个椭圆,则该椭圆的离心率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若关于x的不等式e2x﹣alnx![]() a恒成立,则实数a的取值范围是( )
a恒成立,则实数a的取值范围是( )
A.[0,2e]B.(﹣∞,2e]C.[0,2e2]D.(﹣∞,2e2]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+1|﹣|2x﹣2|的最大值为M,正实数a,b满足a+b=M.
(1)求2a2+b2的最小值;
(2)求证:aabb≥ab.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义域为
是定义域为![]() 的偶函数,对
的偶函数,对![]() ,有
,有![]() ,且当
,且当![]() 时,
时,![]() ,函数
,函数![]() .现给出以下命题:①
.现给出以下命题:①![]() 是周期函数;②
是周期函数;②![]() 的图象关于直线
的图象关于直线![]() 对称;③当
对称;③当![]() 时,
时,![]() 在
在![]() 内有一个零点;④当
内有一个零点;④当![]() 时,
时,![]() 在
在![]() 上至少有六个零.其中正确命题的序号为________.
上至少有六个零.其中正确命题的序号为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com