
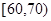 为D等级,有15间;分数在
为D等级,有15间;分数在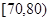 为C等级,有40间;分数在
为C等级,有40间;分数在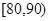 为B等级,有20间;分数在
为B等级,有20间;分数在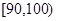 为D等级,有25间. 考核评估后,得其频率直方图如图所示,估计这100间学生公寓评估得分的中位数是
为D等级,有25间. 考核评估后,得其频率直方图如图所示,估计这100间学生公寓评估得分的中位数是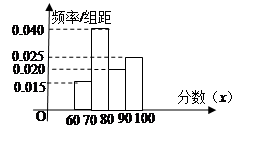
| A.78.65 | B.78.75 | C.78.80 | D.78.85 |
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源:不详 题型:解答题
 ,第二类在
,第二类在 ,第三类在
,第三类在 (单位:千瓦时). 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.
(单位:千瓦时). 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示. 
 为获奖户数,求
为获奖户数,求 的数学期望
的数学期望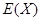 与方差
与方差 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.100 | B.99 | C.98.5 | D.98 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

| A.2827.5 | B.2828.5 |
| C.2927.5 | D.2928.5 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.12,24,15,9 | B.9,12,12,7 |
| C.8,16,10,6 | D.8,15,12,5 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,为了了解这批食品的实际重量情况,从中随机抽取10袋食品,称出各袋的重量(单位:
,为了了解这批食品的实际重量情况,从中随机抽取10袋食品,称出各袋的重量(单位: ),并得到其茎叶图(如图).
),并得到其茎叶图(如图).
 ,则视为不合格产品,试估计这批食品重量的合格率.
,则视为不合格产品,试估计这批食品重量的合格率.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
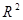 越大,说明残差平方和越小,模型的拟合效果越好;
越大,说明残差平方和越小,模型的拟合效果越好;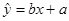 一定过样本点的中心:(
一定过样本点的中心:( ;
;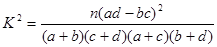 中的
中的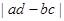 的值越大,说明“两个分类变量有关系”的可能性越强.
的值越大,说明“两个分类变量有关系”的可能性越强.| A.1 | B.3 | C.2 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

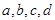 的值;
的值;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com