
【题目】已知函数![]() 图像过点
图像过点![]() ,在
,在![]() 处的切线方程是
处的切线方程是![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)求函数![]() 的图像过点
的图像过点![]() 的切线方程.
的切线方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)把点的坐标![]() ,代入函数解析式中,得到一个方程,对函数求导,根据
,代入函数解析式中,得到一个方程,对函数求导,根据![]() 处的切线方程是
处的切线方程是![]() ,可以求出切点坐标和切线的斜率,这样组成方程组,解方程组即可;
,可以求出切点坐标和切线的斜率,这样组成方程组,解方程组即可;
(2)根据该是不是切点进行分类讨论求解即可.
(1)因为函数![]() 图像过点
图像过点![]() ,所以
,所以![]() .
.
![]() ,在
,在![]() 处的切线方程是
处的切线方程是![]() ,因此切点的坐标为
,因此切点的坐标为![]() ,切线的斜率为4,因此有:
,切线的斜率为4,因此有:![]() ,
,![]() ,三个方程联立得:
,三个方程联立得: ,
,
所以函数的解析式为:![]() ;
;
(2)当点![]() 是切点时,由已知可知,过该点的切线方程为
是切点时,由已知可知,过该点的切线方程为![]() ;
;
当点![]() 不是切点时,设
不是切点时,设![]() 的切点为
的切点为![]() ,
,![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() ,因此过该切点的切线方程为:
,因此过该切点的切线方程为:
![]() ,点
,点![]() 代入该切线方程中得:
代入该切线方程中得:
![]() ,解得
,解得![]() ,或
,或![]() (舍去),所以此时切线方程为:
(舍去),所以此时切线方程为:![]() .
.
综上所述:函数![]() 的图像过点
的图像过点![]() 的切线方程为:
的切线方程为:![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数)曲线
为参数)曲线![]() 的普通方程为
的普通方程为![]() ,以坐标原点为极点,以
,以坐标原点为极点,以![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 和曲线
和曲线![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() :
:![]() 依次与曲线
依次与曲线![]() 和曲线
和曲线![]() 交于
交于![]() 、
、![]() 两点,射线
两点,射线![]() :
:![]() 依次与曲线
依次与曲线![]() 和曲线
和曲线![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司在某市的货物转运中心,拟引进智能机器人分拣系统,以提高分拣效率和降低物流成本,已知购买x台机器人的总成本p(x)=![]() 万元.
万元.
(1)若使每台机器人的平均成本最低,问应买多少台?
(2)现按(1)中的数量购买机器人,需要安排m人将邮件放在机器人上,机器人将邮件送达指定落袋格口完成分拣,经实验知,每台机器人的日平均分拣量q(m)=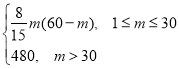 (单位:件),已知传统人工分拣每人每日的平均分拣量为1200件,问引进机器人后,日平均分拣量达最大值时,用人数量比引进机器人前的用人数量最多可减少百分之几?
(单位:件),已知传统人工分拣每人每日的平均分拣量为1200件,问引进机器人后,日平均分拣量达最大值时,用人数量比引进机器人前的用人数量最多可减少百分之几?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A,B是半径为2的圆周上的定点,P为圆周上的动点,![]() 是锐角,大小为β.图中阴影区域的面积的最大值为
是锐角,大小为β.图中阴影区域的面积的最大值为
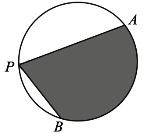
A. 4β+4cosβB. 4β+4sinβC. 2β+2cosβD. 2β+2sinβ
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的中心在原点,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,且过点P
,且过点P![]() 。
。
(1)求椭圆的标准方程;
(2)已知斜率为1的直线l过椭圆的右焦点F交椭圆于A.B两点,求弦AB的长。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,
两点,![]() 为坐标原点,直线
为坐标原点,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,且
,且![]() .
.
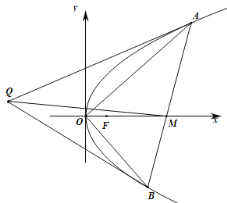
(1)求证:![]() ;
;
(2)求点![]() 的横坐标;
的横坐标;
(3)过![]() 点分别作抛物线的切线,两条切线交于点
点分别作抛物线的切线,两条切线交于点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某养殖场需要通过某装置对养殖车间进行恒温控制,为了解日用电量![]() 与日平均气温
与日平均气温![]() (℃)之间的关系,随机统计了某5天的用电量与当天平均气温,并制作了对照表:
(℃)之间的关系,随机统计了某5天的用电量与当天平均气温,并制作了对照表:
日平均气温(℃) | 3 | 4 | 5 | 6 | 7 |
日用电量( | 2.5 | 3 | 4 | 4.5 | 6 |
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(Ⅱ)请利用(Ⅰ)中的线性回归方程预测日平均气温为12℃时的日用电量.
附:回归直线的斜率和截距的最小二乘法估计公式分别为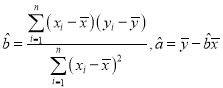 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com