
分析 根据双曲线的定义求出命题p为真时的m的范围,根据椭圆的定义求出命题q为真时的m的范围,从而求出p,q均为假命题时的m的范围.
解答 解:由(1-m)(m+2)<0得:m<-2或m>1,
∴命题p为真,则m<-2或m>1,
由2m>2-m>0得:$\frac{2}{3}$<m<2,
∴命题q为真,则$\frac{2}{3}$<m<2,
∵p∧q是假命题,
∴p是假命题或q是假命题,
由p是假命题得:-2≤m≤1,
则q是假命题得:m≤$\frac{2}{3}$或m≥2,
∴p∧q是假命题时m的取值范围是{m|m≤1或m≥2}.
点评 本题考查了复合命题的判断,考查双曲线以及椭圆的定义,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
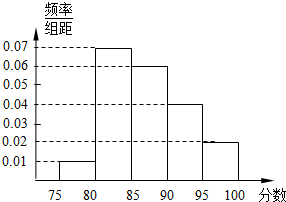 有某单位在2016年的招聘考试中100名竞聘者的笔试成绩,按成绩分组为:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.
有某单位在2016年的招聘考试中100名竞聘者的笔试成绩,按成绩分组为:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若$\overrightarrow{a}$=$\overrightarrow{b}$,$\overrightarrow{b}$=$\overrightarrow{c}$,则$\overrightarrow{a}$=$\overrightarrow{c}$ | B. | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,则$\overrightarrow{a}$=$\overrightarrow{b}$ | ||
| C. | 若λ$\overrightarrow{a}$=0(λ为实数),则λ=0 | D. | 若$\overrightarrow{a}$∥$\overrightarrow{b}$,$\overrightarrow{b}$∥$\overrightarrow{c}$,则$\overrightarrow{a}$∥$\overrightarrow{c}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{9}$=1(y≠0) | B. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1(y≠0) | ||
| C. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1(y≠0) | D. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{16}$=1(y≠0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\overrightarrow{DA}$ | B. | 2$\overrightarrow{AD}$ | C. | 2$\overrightarrow{BD}$ | D. | 2$\overrightarrow{DB}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
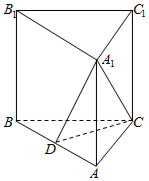 如图,直三棱柱ABC-A1B1C1中,D是AB的中点,AB=2$\sqrt{2}$,AA1=AC=CB=2.
如图,直三棱柱ABC-A1B1C1中,D是AB的中点,AB=2$\sqrt{2}$,AA1=AC=CB=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
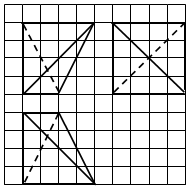 如图,网格纸上小正方形的边长为1,粗线画出的是某四面体的三视图,则该四面体的外接球半径为( )
如图,网格纸上小正方形的边长为1,粗线画出的是某四面体的三视图,则该四面体的外接球半径为( )| A. | 2$\sqrt{2}$ | B. | $\frac{7\sqrt{2}}{3}$ | C. | $\sqrt{11}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com