
【题目】如图1,在等腰梯形![]() 中,两腰
中,两腰![]() ,底边
,底边![]() 是
是![]() 的三等分点,
的三等分点,![]() 是
是![]() 的中点.分别沿
的中点.分别沿![]() 将四边形
将四边形![]() 和
和![]() 折起,使
折起,使![]() 重合于点
重合于点![]() ,得到如图2所示的几何体.在图2中,
,得到如图2所示的几何体.在图2中,![]() 分别为
分别为![]() 的中点.
的中点.
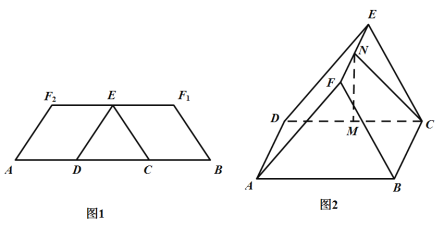
(1)证明:![]() 平面
平面![]()
(2)求几何体![]() 的体积.
的体积.
科目:高中数学 来源: 题型:
【题目】已知直线![]() 、
、![]() 与平面
与平面![]() 、
、![]() 满足
满足![]() ,
,![]() ,
,![]() ,则下列命题中正确的是( )
,则下列命题中正确的是( )
A.![]() 是
是![]() 的充分不必要条件
的充分不必要条件
B.![]() 是
是![]() 的充要条件
的充要条件
C.设![]() ,则
,则![]() 是
是![]() 的必要不充分条件
的必要不充分条件
D.设![]() ,则
,则![]() 是
是![]() 的既不充分也不必要条件
的既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以原点为圆心,椭圆
,以原点为圆心,椭圆![]() 的短半轴长为半径的圆与直线
的短半轴长为半径的圆与直线![]() 相切.
相切.
(Ⅰ)求椭圆方程;
(Ⅱ)设![]() 为椭圆右顶点,过椭圆
为椭圆右顶点,过椭圆![]() 的右焦点的直线
的右焦点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(异于
两点(异于![]() ),直线
),直线![]() ,
,![]() 分别交直线
分别交直线![]() 于
于![]() ,
,![]() 两点. 求证:
两点. 求证:![]() ,
,![]() 两点的纵坐标之积为定值.
两点的纵坐标之积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]()
![]() ,记
,记![]() .
.
(1)若![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() 的最大值;
的最大值;
(2)若![]() ,
,![]() ,且方程
,且方程![]()
![]() 有两个不相等的实根
有两个不相等的实根![]() 、
、![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若![]() ,
,![]() ,
,![]() ,且a、b、c是三角形的三边长,试求满足等式:
,且a、b、c是三角形的三边长,试求满足等式:![]() 有解的最大的x的范围.
有解的最大的x的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
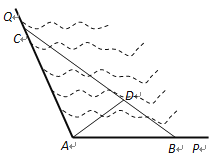
【题目】如图所示,![]() 是某海湾旅游区的一角,其中
是某海湾旅游区的一角,其中![]() ,为了营造更加优美的旅游环境,旅游区管委会决定在直线海岸
,为了营造更加优美的旅游环境,旅游区管委会决定在直线海岸![]() 和
和![]() 上分别修建观光长廊
上分别修建观光长廊![]() 和AC,其中
和AC,其中![]() 是宽长廊,造价是
是宽长廊,造价是![]() 元/米,
元/米,![]() 是窄长廊,造价是
是窄长廊,造价是![]() 元/米,两段长廊的总造价为120万元,同时在线段
元/米,两段长廊的总造价为120万元,同时在线段![]() 上靠近点
上靠近点![]() 的三等分点
的三等分点![]() 处建一个观光平台,并建水上直线通道
处建一个观光平台,并建水上直线通道![]() (平台大小忽略不计),水上通道的造价是
(平台大小忽略不计),水上通道的造价是![]() 元/米.
元/米.
(1) 若规划在三角形![]() 区域内开发水上游乐项目,要求
区域内开发水上游乐项目,要求![]() 的面积最大,那么
的面积最大,那么![]() 和
和![]() 的长度分别为多少米?
的长度分别为多少米?
(2) 在(1)的条件下,建直线通道![]() 还需要多少钱?
还需要多少钱?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,点
中,点![]() ,
,![]() 是曲线
是曲线![]() 上的任意一点,动点
上的任意一点,动点![]() 满足
满足![]()
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)经过点![]() 的动直线
的动直线![]() 与点
与点![]() 的轨迹方程交于
的轨迹方程交于![]() 两点,在
两点,在![]() 轴上是否存在定点
轴上是否存在定点![]() (异于点
(异于点![]() ),使得
),使得![]() ?若存在,求出
?若存在,求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方体![]() 的棱长为2,E、F、G分别为
的棱长为2,E、F、G分别为![]() 的中点,给出下列命题:
的中点,给出下列命题:
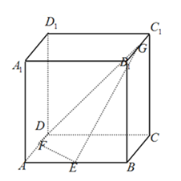
①异面直线EF与AG所成的角的余弦值为![]() ;
;
②过点E、F、G作正方体的截面,所得的截面的面积是![]() ;
;
③![]() 平面
平面![]()
④三棱锥![]() 的体积为1
的体积为1
其中正确的命题是_____________(填写所有正确的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆
,圆![]() ,动圆P与圆M外切并且与圆N内切,圆心P的轨迹为曲线C.
,动圆P与圆M外切并且与圆N内切,圆心P的轨迹为曲线C.
(1)求曲线C的方程;
(2)设不经过点![]() 的直线l与曲线C相交于A,B两点,直线QA与直线QB的斜率均存在且斜率之和为-2,证明:直线l过定点.
的直线l与曲线C相交于A,B两点,直线QA与直线QB的斜率均存在且斜率之和为-2,证明:直线l过定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com