练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某教育主管部门到一所中学检查高三年级学生的体质健康情况，从中抽取了名学生的体质测试成绩，得到的频率分布直方图如图1所示，样本中前三组学生的原始成绩按性别分类所得的茎叶图如图2所示.

    （Ⅰ）求， ， 的值；

    （Ⅱ）估计该校高三学生体质测试成绩的平均数和中位数；

    （Ⅲ）若从成绩在的学生中随机抽取两人重新进行测试，求至少有一名男生的概率.

    【答案】（Ⅰ）.

    （Ⅱ）.

    （Ⅲ）.

    【解析】试题分析：（Ⅰ）由茎叶图可知分数在的有人，进而求解的值；

    （Ⅱ）根据数据平均数的计算公式，即可求得的值．

    （Ⅲ）两名男生分别记为， ，四名女生分别记为， ， ， ，列举出从中任取两人的基本事件的总数，即可利用古典概率的概率计算公式求解概率．

    试题解析：

    （Ⅰ）由茎叶图可知分数在的有4人，

    所以， ， ，

    解得.

    （Ⅱ） ，

    由 ，得.

    （Ⅲ）两名男生分别记为， ，四名女生分别记为， ， ， ，

    从中任取两人共有， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ，共15种结果，至少有一名男生的结果有， ， ， ， ， ， ， ， ，共9种结果，所以至少有一名男生的概率为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知平面向量=(1，x)，=(2x+3，-x)，x∈R.

    （1）若⊥，求x的值；

    （2）若∥，求|-|的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数是上的奇函数．

    (1)求的值；

    (2)证明在上单调递减；

    (3)若对任意的，不等式恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下列四个命题：

    ①函数y=2sin的图象的一条对称轴是x=；

    ②函数y=tanx的图象关于点对称；

    ③若sin=sin，则x1-x2=kπ，其中k∈Z；

    ④函数，x∈[0，2π]的图象与直线y=k有且仅有两个不同的交点，则k的取值范围为(1，3).

    其中正确的有____(填写所有正确命题的序号).

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数。

    （1）若函数在处的切线垂直于轴，求实数的值；

    （2）在（1）的条件下，求函数的单调区间；

    （3）若时，恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】国际奥委会将于2017年9月15日在秘鲁利马召开130次会议决定2024年第33届奥运会举办地，目前德国汉堡，美国波士顿等申办城市因市民担心赛事费用超支而相继退出，某机构为调查我国公民对申办奥运会的态度，选了某小区的100位居民调查结果统计如下：

    支持

    不支持

    合计

    年龄不大于50岁

    80

    年龄大于50岁

    10

    合计

    70

    100

    （1）根据已知数据，把表格数据填写完整；

    （2）能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运有关？

    （3）已知在被调查的年龄大于50岁的支持者中有5名女性，其中2位是女教师，现从这5名女性中随机抽取3人，求至多有1位教师的概率.

    附： ， ，

    0.100

    0.050

    0.025

    0.010

    2.706

    3.841

    5.024

    6.635

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】正方体ABCD - A1B1C1D1的棱长为2， E、F、G分别为BC、CC1、BB1的中点，则（ ）

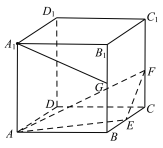
    A.直线与直线AF垂直B.直线A1G与平面AEF平行

    C.平面截正方体所得的截面面积为D.点C与点G到平面AEF的距离相等

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线的参数方程为（为参数），将曲线上各点的横坐标都缩短为原来的倍，纵坐标坐标都伸长为原来的倍，得到曲线，在极坐标系（与直角坐标系取相同的单位长度，且以原点为极点，以轴非负半轴为极轴）中，直线的极坐标方程为．

    （1）求直线和曲线的直角坐标方程；

    （2）设点是曲线上的一个动点，求它到直线的距离的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市场研究人员为了了解产业园引进的甲公司前期的经营状况，对该公司2019年连续六个月（5-10）月）的利润进行了统计，并根据得到的数据绘制了相应的折线图，如图所示.

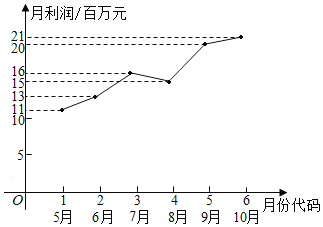
    （1）由折线图可以看出，可用线性回归模型拟合月利润（单位：百万元）与月份代码之间的关系，求关于的线性回归方程，并据此预测该公司2020年5月份的利润；

    （2）甲公司新研制了一款产品，需要采购一批新型材料，现有两种型号的新型材料可供选择，按规定每种新型材料最多可使用4个月，但新材料的不稳定性会导致材料损坏的年限不同，现对两种型号的新型材料对应的产品各100件进行科学模拟测试，得到两种新型材料使用寿命的频数统计表（表）.若从产品使用寿命的角度考虑，甲公司的负责人选择采购哪款新型材料更好？

    使用寿命

    1个月

    2个月

    3个月

    4个月

    总计

    材料类型

    20

    35

    35

    10

    100

    10

    30

    40

    20

    100

    参考数据：，.

    参考公式：回归直线方程，其中，.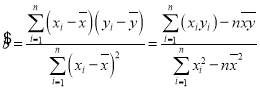

    查看答案和解析>>

    同步练习册答案