练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知向量a＝(cosx，sinx)，b＝(cos，sin)，c＝(，－1)，其中x∈R，

    (1)当a·b＝时，求x值的集合；

    (2)设函数f(x)＝(a－c)2，求f(x)的最小正周期及其单调增区间.

    【解析】(1)∵a·b＝cos·cos－sinsin＝cos2x＝，

    ∴2x＝2kπ±，x＝kπ±(k∈Z)，

    ∴x的集合是{x|x＝kπ±(k∈Z)}.

    (2)∵a－c＝(cos－，sin＋1)，

    ∴f(x)＝(cos－)2＋(sin＋1)2＝2＋3－2cos＋2sin

    ＝5＋4(sin－cos)＝5＋4sin(－).

    ①最小正周期T＝＝π；

    ②2kπ－≤－≤2kπ＋，即2kπ－≤≤2kπ＋，

    kπ－≤x≤kπ＋π(k∈Z)，

    ∴f(x)的单调增区间是[kπ－，kπ＋](k∈Z).

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：新课程高中数学疑难全解 题型：022

    已知向量a＝(cosθ，sinθ)，向量b＝(，－1)，则|2a－b|的最大值、最小值分别是________．

    查看答案和解析>>

    科目：高中数学 来源：高考总复习全解　数学　一轮复习·必修课程　（人教实验版）　B版 人教实验版　B版 题型：022

    已知向量a＝(cosθ，sinθ)，向量b＝(，－1)，则|2a－b|的最大值是________．

    查看答案和解析>>

    科目：高中数学 来源：2009届广东四校联考数学文科试卷及答案 题型：022

    已知向量a＝(cosa ，sina )，b＝(cosb ，sinb )，|a＋b|＝|a－b|且a≠±b，那么a与b的夹角的大小为________．

    查看答案和解析>>

    科目：高中数学 来源：2012人教A版高中数学必修四3.1两角和差的正弦余弦和正切公式（二）（解析版） 题型：解答题

    已知向量a＝(cosα，sinα)，b＝(cosβ，sinβ)，|a－b|＝.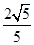

    (1)求cos(α－β)的值；

    (2)若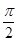－<β<0<α<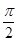，且sinβ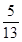＝－，求sinα的值．

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年重庆市高三11月月考文科数学 题型：填空题

    已知向量a＝(cosθ，sinθ)，b＝(cosφ，sinφ)，若θ－φ＝，则向量a与向量a＋b的夹角是____________．

     

    查看答案和解析>>

    同步练习册答案