
【题目】某地有A,B、C、D四人先后感染了新型冠状病毒,其中只有A到过疫区,B肯定是受A感染的,对于C,因为难以判定他是受A还是受B感染的,于是假定他受A和受B感染的概率都是![]() ,同样也假设D受A、B和C感染的概率都是
,同样也假设D受A、B和C感染的概率都是![]() .在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量,写出X的可能取值为______,并求X的均值(即数学期望)为______.
.在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量,写出X的可能取值为______,并求X的均值(即数学期望)为______.
【答案】1,2,3 ![]()
【解析】
由题意得X可取的值为1、2、3,用“![]() ”(
”(![]() 、2、3)表示被A直接感染的人数.先明确四个人的传染情形共有6种:
、2、3)表示被A直接感染的人数.先明确四个人的传染情形共有6种:![]() ,
,
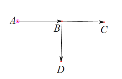 ,
, ,
, ,
, ,
,
每种情况发生的可能性都相等,可以得到A传染1人有两种情况,传染2人有三种情况,传染3人有一种情况,分别求得其发生的概率,列车分布列再求期望.
由题意得X可取的值为1、2、3,
用“![]() ”(
”(![]() 、2、3)表示被A直接感染的人数.
、2、3)表示被A直接感染的人数.
四个人的传染情形共有6种:![]() ,
,
 ,
, ,
, ,
, ,
,
每种情况发生的可能性都相等,
所以A传染1人有两种情况,传染2人有三种情况,传染3人有一种情况.
“![]() ”表示A传染B,没有传染给C、D:
”表示A传染B,没有传染给C、D:
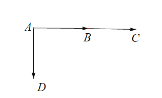
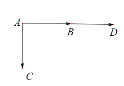
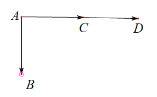
“![]() ”表示A传染给B、C,没有传染给D,或A传染给B、D,没有传染给C:
”表示A传染给B、C,没有传染给D,或A传染给B、D,没有传染给C:
“![]() ”表示A传染给B、C、D.
”表示A传染给B、C、D.
于是有:
![]() ,
,
![]() ,
,
![]() .
.
分布列为
X | 1 | 2 | 3 |
P |
|
|
|
![]()
故答案为:(1). 1,2,3 (2). ![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】微信是腾讯公司推出的一种手机通讯软件,一经推出便风靡全国,甚至涌现出一批在微信的朋友圈内销售商品的人(被称为微商).为了调查每天微信用户使用微信的时间,某经销化妆品的微商在一广场随机采访男性、女性用户各50名,其中每天玩微信超过6小时的用户为“![]() 组”,否则为“
组”,否则为“![]() 组”,调查结果如下:
组”,调查结果如下:

(1)根据以上数据,能否有60%的把握认为“![]() 组”用户与“性别”有关?
组”用户与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人赠送营养面膜1份,求所抽取5人中“![]() 组”和“
组”和“![]() 组”的人数;
组”的人数;
(3)从(2)中抽取的5人中再随机抽取3人赠送200元的护肤品套装,记这3人中在“![]() 组”的人数为
组”的人数为![]() ,试求
,试求![]() 的分布列与数学期望.
的分布列与数学期望.
参考公式: 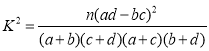 ,其中
,其中![]() .
.
临界值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某花卉经销商销售某种鲜花,售价为每支5元,成本为每支2元.销售宗旨是当天进货当天销售.当天未售出的当垃圾处理.根据以往的销售情况,按![]()
![]()
![]()
![]()
![]() 进行分组,得到如图所示的频率分布直方图.
进行分组,得到如图所示的频率分布直方图.
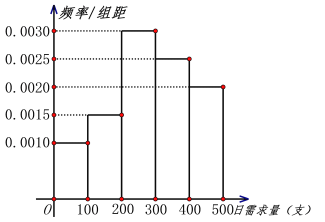
(1)根据频率分布直方图计算该种鲜花日需求量的平均数![]() ,同一组中的数据用该组区间中点值代表;
,同一组中的数据用该组区间中点值代表;
(2)该经销商某天购进了400支这种鲜花,假设当天的需求量为x枝,![]() ,利润为y元,求
,利润为y元,求![]() 关于
关于![]() 的函数关系式,并结合频率分布直方图估计利润
的函数关系式,并结合频率分布直方图估计利润![]() 不小于800元的概率.
不小于800元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地区观众对大型综艺活动《中国好声音》的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众收看该节目的场数与所对应的人数表:

将收看该节目场次不低于13场的观众称为“歌迷”,已知“歌迷”中有10名女性.
(1)根据已知条件完成下面的2×2列联表
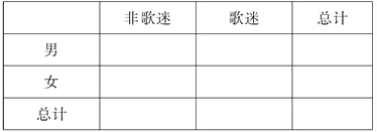
(2)此资料我们能否有95%的把握认为“歌迷”与性别有关?

附: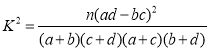
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有![]() 件产品,其中
件产品,其中![]() 件是次品,其余都是合格品,现不放回的从中依次抽
件是次品,其余都是合格品,现不放回的从中依次抽![]() 件.求:(1)第一次抽到次品的概率;
件.求:(1)第一次抽到次品的概率;
(2)第一次和第二次都抽到次品的概率;
(3)在第一次抽到次品的条件下,第二次抽到次品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 元集合
元集合![]() 的一些子集满足:每个子集至少含2个元素,每两个不同子集的交集至多含2个元素,记这些子集的元素个数的立方和为
的一些子集满足:每个子集至少含2个元素,每两个不同子集的交集至多含2个元素,记这些子集的元素个数的立方和为![]() .问:是否存在不小于3的正整数
.问:是否存在不小于3的正整数![]() ,使
,使![]() 的最大值等于2009的方幂?说明你的理由.
的最大值等于2009的方幂?说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 个人在某个节日期间互通电话问候,已知其中每个人至多打通了三个朋友家的电话,任何两个人之间至多进行一次通话,且任何三个人中至少有两人,其中一个人打通了另一个人家里的电话,求
个人在某个节日期间互通电话问候,已知其中每个人至多打通了三个朋友家的电话,任何两个人之间至多进行一次通话,且任何三个人中至少有两人,其中一个人打通了另一个人家里的电话,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点在坐标原点,其焦点
的顶点在坐标原点,其焦点![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() 为直线
为直线![]() 上一点,圆
上一点,圆![]() 与
与![]() 轴相切(
轴相切(![]() 为圆心),且
为圆心),且![]() ,
,![]() 关于点
关于点![]() 对称.
对称.
(1)求圆![]() 和抛物线
和抛物线![]() 的标准方程;
的标准方程;
(2)过![]() 的直线
的直线![]() 交圆
交圆![]() 于
于![]() ,
,![]() 两点,交抛物线
两点,交抛物线![]() 于
于![]() ,
,![]() 两点,求证:
两点,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com