
����Ŀ���躯��y=f��x��ͼ���ϲ�ͬ����A��x1 �� y1����B��x2 �� y2���������ߵ�б�ʷֱ���kA �� kB �� �涨�գ�A��B��= ![]() ��|AB|Ϊ�߶�AB�ij��ȣ���������y=f��x���ڵ�A���B֮��ġ������ȡ��������������⣺ �ٺ���y=x3ͼ��������A��B�ĺ�����ֱ�Ϊ1�ͩ�1����գ�A��B��=0��
��|AB|Ϊ�߶�AB�ij��ȣ���������y=f��x���ڵ�A���B֮��ġ������ȡ��������������⣺ �ٺ���y=x3ͼ��������A��B�ĺ�����ֱ�Ϊ1�ͩ�1����գ�A��B��=0��
�ڴ��������ĺ�����ͼ������������֮��ġ������ȡ�Ϊ������
�����A��B��������y=x2+1�ϲ�ͬ�����㣬��գ�A��B����2��
��������y=ex��e����Ȼ�����ĵ������ϲ�ͬ����A��x1 �� y1����B��x2 �� y2������գ�A��B����1��
��������������Ϊ �� �����������������Ŷ����ϣ�
���𰸡��٢ڢۢ�
���������⣺���ڢ٣���y=x3����y��=3x2��
��kA=3��kB=3����|kA��kB|=0����գ�A��B��=0���ʢ���ȷ��
���ڢڣ���y=1ʱ��y��=0����գ�A��B��=0���ʢ���ȷ��
���ڢۣ�������y=x2+1�ĵ���Ϊy��=2x��yA=xA2+1��yB=xB2+1��
yA��yB=xA2��xB2=��xA��xB����xA+xB����
��գ�A��B��= ![]() =
= ![]() =
= ![]() ��2���ʢ���ȷ��
��2���ʢ���ȷ��
���ڢܣ���y=ex����y��=ex���գ�A��B��= 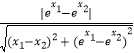 ��
��
�ɲ�ͬ����A��x1��y1����B��x2��y2�����ɵæգ�A��B���� 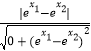 =1��
=1��
�ʢ���ȷ��
���Դ��ǣ��٢ڢۢ�
�����㾫����������Ŀ����֪�������������������ж���Ӧ�õ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ�����������⻥Ϊ������⣬��������ͬ������ԣ���������Ϊ������������⣬���ǵ������û�й�ϵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������![]() �У�����
�У�����![]() Ϊ���Σ�
Ϊ���Σ� ![]() ƽ��
ƽ��![]() ��
�� ![]() ����
����![]() Ϊ
Ϊ![]() ���е㣮
���е㣮
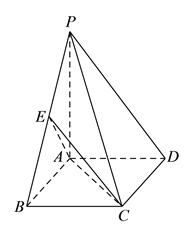
��![]() ����֤��
����֤�� ![]() ƽ��
ƽ��![]() ��
��
��![]() ����֤��ƽ��
����֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=ax2+2x��2��a��a��0����
��1����a=��1����������㣻
��2�������������䣨0��1]��ǡ��һ����㣬��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ԲC��x2+y2=4��ֱ��l��y=x����ԲC����ȡһ��A��ֱ��l�ľ���С��1�ĸ���Ϊ�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������P��ABCD�У�����ABCD�Ǿ��Σ���AD=2��AB=1��PA��ƽ��ABCD��E��F�ֱ����߶�AB��BC���е㣮 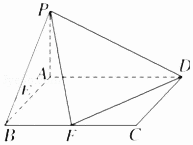
��1��֤����PF��FD��
��2����PA=1�����E��ƽ��PFD�ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=lnx+ ![]() ax2��2x���ڵ����ݼ����䣬��ʵ��a��ȡֵ��ΧΪ ��
ax2��2x���ڵ����ݼ����䣬��ʵ��a��ȡֵ��ΧΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��֯������һ����,����ֳ��ȵ���ά��ռ�ı������±���ʾ:

(1)�������������ά��ƽ�������뷽��.
(2)����涨��������ά��ƽ������Ϊ4.90����,�������1.200,������������������0.10��Ϊ�ϸ��Ʒ.��������������������Ƿ�ϸ�?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x2��ax��aln��x��1����a��R��
��1����a=1ʱ������f��x������ֵ��
��2������f��x���ĵ������䣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com