
【题目】已知函数f(x)=(x﹣1)2﹣alnx(a<0).
(1)讨论f(x)的单调性;
(2)若f(x)存在两个极值点x1,x2(x1<x2),且关于x的方程f(x)=b(b∈R)恰有三个实数根x3,x4,x5(x3<x4<x5),求证:2(x2﹣x1)>x5﹣x3.
【答案】(1)答案不唯一,具体见解析(2)证明见解析
【解析】
(1)求导得f′(x)![]() ,令f′(x)=0,即2x2﹣2x﹣a=0,
,令f′(x)=0,即2x2﹣2x﹣a=0,![]() =4+8a,分两种情况①
=4+8a,分两种情况①![]() ≤0,②
≤0,②![]() >0,讨论f(x)单调性;
>0,讨论f(x)单调性;
(2)由题意得![]() a<0,画出草图,知0<x3<x1<x4<x2<x5,0<x1<x2<1,要证:2(x2﹣x1)>x5﹣x3,即证:2(x2﹣x1)>(x5+x4)﹣(x3+x4),只需证:
a<0,画出草图,知0<x3<x1<x4<x2<x5,0<x1<x2<1,要证:2(x2﹣x1)>x5﹣x3,即证:2(x2﹣x1)>(x5+x4)﹣(x3+x4),只需证: ,先证:x3+x4>2x1.即证x4>2x1﹣x3,由(1)f(x)单调递减,只需证f(x4)<f(2x1﹣x3),即证:f(x3)<f(2x1﹣x3),令g(x)=f(x)﹣f(2x1﹣x),0<x<x1,求导数,分析单调性,可得g(x)<g(x1)=0,故f(x)<f(2x1﹣x),在(0,x1)恒成立,f(x3)<f(2x1﹣x3)得证,同理可以证明:x3+x4<2x2,综上,2(x2﹣x1)>x5﹣x3,得证.
,先证:x3+x4>2x1.即证x4>2x1﹣x3,由(1)f(x)单调递减,只需证f(x4)<f(2x1﹣x3),即证:f(x3)<f(2x1﹣x3),令g(x)=f(x)﹣f(2x1﹣x),0<x<x1,求导数,分析单调性,可得g(x)<g(x1)=0,故f(x)<f(2x1﹣x),在(0,x1)恒成立,f(x3)<f(2x1﹣x3)得证,同理可以证明:x3+x4<2x2,综上,2(x2﹣x1)>x5﹣x3,得证.
(1)由题意得![]() =2(x﹣1)
=2(x﹣1)![]() ,
,
令![]() =0,即2x2﹣2x﹣a=0,
=0,即2x2﹣2x﹣a=0,![]() =4+8a,
=4+8a,
①当a![]() 时,
时,![]() ≤0,
≤0,![]() ≥0,函数f(x)在(0,+∞)上单调递增,
≥0,函数f(x)在(0,+∞)上单调递增,
②当![]() a<0时,
a<0时,![]() >0,
>0,
2x2﹣2x﹣a=0的两根为x1![]() ,x2
,x2![]() 且0<x1
且0<x1![]() x2,
x2,
当x∈(0,![]() ),(
),(![]() ,+∞)时,
,+∞)时,![]() >0,f(x)单调递增,
>0,f(x)单调递增,
当x∈(![]() ,
,![]() )时,
)时,![]() <0,f(x)单调递减,
<0,f(x)单调递减,
综上,当a![]() 时,函数f(x)在(0,+∞)上单调递增,
时,函数f(x)在(0,+∞)上单调递增,
当![]() a<0时,f(x)在(0,
a<0时,f(x)在(0,![]() )上单调递增,在(
)上单调递增,在(![]() ,
,![]() )上单调递减,在(
)上单调递减,在(![]() ,+∞)上单调递增.
,+∞)上单调递增.
(2)证明:由题意得![]() a<0,0<x3<x1<x4<x2<x5,0<x1<x2<1,如图,
a<0,0<x3<x1<x4<x2<x5,0<x1<x2<1,如图,
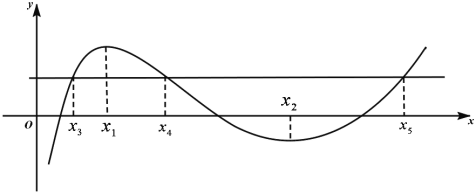
要证:2(x2﹣x1)>x5﹣x3,
即证:2(x2﹣x1)>(x5+x4)﹣(x3+x4);
只需证:
先证:x3+x4>2x1.
即证x4>2x1﹣x3,
又由(1)知f(x)在(x1,x2)上单调递减,
只需证f(x4)<f(2x1﹣x3),
而f(x4)=f(x3),即证:f(x3)<f(2x1﹣x3),
令g(x)=f(x)﹣f(2x1﹣x),0<x<x1,
![]() =
=![]() +
+![]() =2x﹣2
=2x﹣2![]() 2(2x1﹣x)﹣2
2(2x1﹣x)﹣2![]() ,
,
=4(x1﹣1)![]()
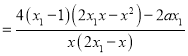
又2(x1﹣1)![]() 0,即x1﹣1
0,即x1﹣1![]() ,那么,
,那么,
![]()
 ,而0<x<x1,且
,而0<x<x1,且![]() ,
,
则![]() >0,故g(x)在(0,x1)单调递增,则g(x)<g(x1)=0,
>0,故g(x)在(0,x1)单调递增,则g(x)<g(x1)=0,
故f(x)<f(2x1﹣x),在(0,x1)恒成立,
又0<x3<x1,则f(x3)<f(2x1﹣x3)得证,
同理可以证明:x3+x4<2x2,
综上,2(x2﹣x1)>x5﹣x3,得证.


科目:高中数学 来源: 题型:
【题目】对两个变量![]() 与
与![]() 进行线性相关性和回归效果分析,得到一组样本数据:
进行线性相关性和回归效果分析,得到一组样本数据:![]() 、
、![]() 、
、![]() 、
、![]() ,则下列说法不正确的是( )
,则下列说法不正确的是( )
A.残差平方和越小的模型,拟合的效果越好
B.由样本数据利用最小二乘法得到的回归方程表示的直线必过样本点的中心![]()
C.若变量![]() 与
与![]() 之间的相关系数
之间的相关系数![]() ,则变量
,则变量![]() 与
与![]() 之间具有很强的线性相关性
之间具有很强的线性相关性
D.用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越小,说明模型的拟合效果越好
越小,说明模型的拟合效果越好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一“T”型水渠的平面视图(俯视图),水渠的南北方向和东西方向轴截面均为矩形,南北向渠宽为4m,东西向渠宽![]() m(从拐角处,即图中
m(从拐角处,即图中![]() ,
,![]() 处开始).假定渠内的水面始终保持水平位置(即无高度差).
处开始).假定渠内的水面始终保持水平位置(即无高度差).
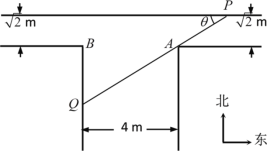
(1)在水平面内,过点![]() 的一条直线与水渠的内壁交于
的一条直线与水渠的内壁交于![]() ,
,![]() 两点,且与水渠的一边的夹角为
两点,且与水渠的一边的夹角为![]() ,将线段
,将线段![]() 的长度
的长度![]() 表示为
表示为![]() 的函数;
的函数;
(2)若从南面漂来一根长为7m的笔直的竹竿(粗细不计),竹竿始终浮于水平面内,且不发生形变,问:这根竹竿能否从拐角处一直漂向东西向的水渠(不会卡住)?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知梯形ABCD满足AB∥CD,∠BAD=45°,以A,D为焦点的双曲线Γ经过B,C两点.若CD=7AB,则双曲线Γ的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校的一个社会实践调查小组,在对该校学生的良好“用眼习惯”的调查中,随机发放了120分问卷.对收回的100份有效问卷进行统计,得到如![]() 下列联表:
下列联表:
做不到科学用眼 | 能做到科学用眼 | 合计 | |
男 | 45 | 10 | 55 |
女 | 30 | 15 | 45 |
合计 | 75 | 25 | 100 |
(1)现按女生是否能做到科学用眼进行分层,从45份女生问卷中抽取了6份问卷,从这6份问卷中再随机抽取3份,并记其中能做到科学用眼的问卷的份数![]() ,试求随机变量
,试求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若在犯错误的概率不超过![]() 的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的
的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的![]() 的值应为多少?请说明理由.
的值应为多少?请说明理由.
附:独立性检验统计量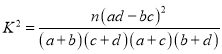 ,其中
,其中![]() .
.
独立性检验临界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人各射击一次,击中目标的概率分别是![]() 和
和![]() ,假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响.
,假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响.
(1)求甲射击4次,至多1次未击中目标的概率;
(2)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(3)假设某人连续2次未击中目标,则停止射击,求乙恰好射击5次后被中止射击的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com