
【题目】函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ< ![]() )的图象与y轴的交点为(0,
)的图象与y轴的交点为(0, ![]() ),它的一个对称中心是M(
),它的一个对称中心是M( ![]() ,0),点M与最近的一条对称轴的距离是
,0),点M与最近的一条对称轴的距离是 ![]() .
.
(1)求此函数的解析式;
(2)求此函数取得最大值时x的取值集合;
(3)当x∈(0,π)时,求此函数的单调递增区间.
【答案】
(1)解:函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ< ![]() )的图象
)的图象
的一个对称中心是M( ![]() ,0),点M与最近的一条对称轴的距离是
,0),点M与最近的一条对称轴的距离是 ![]() ,故
,故  ,
,
求得ω=2,φ= ![]() .
.
再根据函数的图象与y轴的交点为(0, ![]() ),可得Asin(ω0+
),可得Asin(ω0+ ![]() )=
)= ![]() ,∴A=2,
,∴A=2,
函数f(x)=2sin(2x+ ![]() ).
).
(2)解:令2x+ ![]() =2kπ+
=2kπ+ ![]() ,求得 x=kπ+
,求得 x=kπ+ ![]() ,k∈Z,故函数取得最大值时x的取值集合为{x|x=kπ+
,k∈Z,故函数取得最大值时x的取值集合为{x|x=kπ+ ![]() ,k∈Z}
,k∈Z}
(3)解:令2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,求得kπ﹣
,求得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,可得函数的增区间为[2kπ﹣
,可得函数的增区间为[2kπ﹣ ![]() ,2kπ+
,2kπ+ ![]() ],k∈Z.
],k∈Z.
再结合x∈(0,π),可得函数的增区间为(0, ![]() ]、[
]、[ ![]() ,π)
,π)
【解析】(1)由函数的周期性、图象的对称性求出ω、φ的值,由特殊点的坐标求出A的值,可得函数的解析式.(2)利用正弦函数的最大值,求得函数取得最大值时x的取值集合.(3)利用正弦函数的调增区间,求得当x∈(0,π)时,此函数的单调递增区间.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源: 题型:
【题目】如图,我国南海某处的一个圆形海域上有四个小岛,小岛B与小岛A、小岛C相距都为5n mile,与小岛D相距为 ![]() n mile.小岛A对小岛B与D的视角为钝角,且
n mile.小岛A对小岛B与D的视角为钝角,且 ![]() .
.
(Ⅰ)求小岛A与小岛D之间的距离和四个小岛所形成的四边形的面积;
(Ⅱ)记小岛D对小岛B与C的视角为α,小岛B对小岛C与D的视角为β,求sin(2α+β)的值.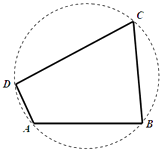
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知长方体ABCD﹣A1B1C1D1中,AB=BC=2,AA1=4,E是棱CC1上的点,且BE⊥B1C.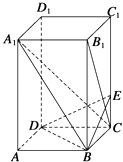
(1)求CE的长;
(2)求证:A1C⊥平面BED;
(3)求A1B与平面BDE夹角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下命题中,正确命题的序号是 . ①函数y=tanx在定义域内是增函数;
②函数y=2sin(2x+ ![]() )的图象关于x=
)的图象关于x= ![]() 成轴对称;
成轴对称;
③已知 ![]() =(3,4),
=(3,4), ![]()
![]() =﹣2,则向量
=﹣2,则向量 ![]() 在向量
在向量 ![]() 的方向上的投影是﹣
的方向上的投影是﹣ ![]()
④如果函数f(x)=ax2﹣2x﹣3在区间(﹣∞,4)上是单调递减的,则实数a的取值范围是(0, ![]() ].
].
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一块大型的广告宣传版面,其形状如图所示的直角梯形![]() .某厂家因产品宣传的需要,拟出资规划出一块区域(图中阴影部分)为产品做广告,形状为直角梯形
.某厂家因产品宣传的需要,拟出资规划出一块区域(图中阴影部分)为产品做广告,形状为直角梯形![]() (点
(点![]() 在曲线段
在曲线段![]() 上,点
上,点![]() 在线段
在线段![]() 上).已知
上).已知![]() ,
,![]() ,其中曲线段
,其中曲线段![]() 是以
是以![]() 为顶点,
为顶点,![]() 为对称轴的抛物线的一部分.
为对称轴的抛物线的一部分.

(1)求线段![]() ,线段
,线段![]() ,曲线段
,曲线段![]() 所围成区域的面积;
所围成区域的面积;
(2)求厂家广告区域![]() 的最大面积.
的最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将边长为![]() 的等边
的等边![]() 沿
沿![]() 轴正方向滚动,某时刻
轴正方向滚动,某时刻![]() 与坐标原点重合(如图),设顶点
与坐标原点重合(如图),设顶点![]() 的轨迹方程是
的轨迹方程是![]() ,关于函数
,关于函数![]() 有下列说法:
有下列说法:

(1)![]() 的值域为
的值域为![]() ;
;
(2)![]() 是周期函数且周期为
是周期函数且周期为![]() ;
;
(3)![]() ;
;
(4)滚动后,当顶点![]() 第一次落在
第一次落在![]() 轴上时,
轴上时,![]() 的图象与
的图象与![]() 轴所围成的面积为
轴所围成的面积为![]()
其中正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为得到函数 ![]() 的图象,只需将函数y=sin2x的图象( )
的图象,只需将函数y=sin2x的图象( )
A.向左平移 ![]() 个长度单位
个长度单位
B.向右平移 ![]() 个长度单位
个长度单位
C.向左平移 ![]() 个长度单位
个长度单位
D.向右平移 ![]() 个长度单位
个长度单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是由
是由![]() 个有序实数构成的一个数组,记作
个有序实数构成的一个数组,记作![]() ,其中
,其中![]()
![]()
![]() 称为数组
称为数组![]() 的“元”,
的“元”, ![]() 称为
称为![]() 的下标,如果数组
的下标,如果数组![]() 中的每个“元”都是来自数组
中的每个“元”都是来自数组
![]() 中不同下标的“元”,则称
中不同下标的“元”,则称![]() 为
为![]() 的子数组,定义两个数组
的子数组,定义两个数组![]() 和
和![]()
![]() 的关系数为
的关系数为![]() ;
;
(1)若![]() ,
, ![]() ,设
,设![]() 是
是![]() 的含有两个“元”的子数组,求
的含有两个“元”的子数组,求![]()
的最大值;
(2)若 ,
, ![]() ,且
,且![]() ,
, ![]() 为
为![]() 的含有三个“元”
的含有三个“元”
的子数组,求![]() 的最大值;
的最大值;
(3)若数组![]() 中的“元”满足
中的“元”满足![]() ,设数组
,设数组![]()
![]() 含有
含有
四个“元”![]() ,且
,且![]() ,求
,求![]() 与
与![]() 的所有含有三个“元”
的所有含有三个“元”
的子数组的关系数的最大值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(文)已知点D(1, ![]() )在双曲线C:
)在双曲线C: ![]() =1(a>0,b>0)上,且双曲线的一条渐近线的方程是
=1(a>0,b>0)上,且双曲线的一条渐近线的方程是 ![]() x+y=0.
x+y=0.
(1)求双曲线C的方程;
(2)若过点(0,1)且斜率为k的直线l与双曲线C有两个不同交点,求实数k的取值范围;
(3)设(2)中直线l与双曲线C交于A、B两个不同点,若以线段AB为直径的圆经过坐标原点,求实数k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com