
(2009年上海卷理)(本题满分18分)本题共有3个小题,第1小题满分5分,第2小题满分5分,第3小题满分8分。
已知![]() 是公差为
是公差为![]() 的等差数列,
的等差数列,![]() 是公比为
是公比为![]() 的等比数列。
的等比数列。
若![]() ,是否存在
,是否存在![]() ,有
,有![]() 说明理由;
说明理由;
找出所有数列![]() 和
和![]() ,使对一切
,使对一切![]() ,
,![]() ,并说明理由;
,并说明理由;
若![]() 试确定所有的
试确定所有的![]() ,使数列
,使数列![]() 中存在某个连续
中存在某个连续![]() 项的和是数列
项的和是数列![]() 中的一项,请证明。
中的一项,请证明。
[解法一](1)由![]() ,得
,得![]() , ......2分
, ......2分
整理后,可得![]() ,
,![]()
![]() 、
、![]()
![]()
![]() ,
,![]()
![]() 为整数,
为整数,
![]() 不存在
不存在![]() 、
、![]()
![]()
![]() ,使等式成立。 ......5分
,使等式成立。 ......5分
(2)若![]() ,即
,即![]() , (*)
, (*)
(ⅰ)若![]() 则
则![]() 。
。
当{![]() }为非零常数列,{
}为非零常数列,{![]() }为恒等于1的常数列,满足要求。 ......7分
}为恒等于1的常数列,满足要求。 ......7分
(ⅱ)若![]() ,(*)式等号左边取极限得
,(*)式等号左边取极限得![]() ,(*)式等号右边的极限只有当
,(*)式等号右边的极限只有当![]() 时,才能等于1。此时等号左边是常数,
时,才能等于1。此时等号左边是常数,![]() ,矛盾。
,矛盾。
综上所述,只有当{![]() }为非零常数列,{
}为非零常数列,{![]() }为恒等于1的常数列,满足要求。......10分
}为恒等于1的常数列,满足要求。......10分
【解法二】设![]()
则![]()
![]()
![]()
若d=0,则![]()
若![]()
![]() (常数)即
(常数)即![]() ,则d=0,矛盾
,则d=0,矛盾
综上所述,有![]() , 10分
, 10分
(3)![]()
设![]() .
.
![]() ,
,
![]() . 13分
. 13分
取![]() 15分
15分
由二项展开式可得正整数M1、M2,使得(4-1)2s+2=4M1+1,
![]()
![]()
故当且仅当p=3s,s![]() N时,命题成立. .
N时,命题成立. .
说明:第(3)题若学生从以下角度解题,可分别得部分分(即分步得分)
若p为偶数,则am+1+am+2+……+am+p为偶数,但3k为奇数
故此等式不成立,所以,p一定为奇数。
当p=1时,则am+1=bk,即4m+5=3k,
而3k=(4-1)k
=![]()
当k为偶数时,存在m,使4m+5=3k成立 1分
当p=3时,则am+1+am+2+am+3=bk,即3am+2-bk,
也即3(4m+9)=3k,所以4m+9=3k-1,4(m+1)+5=3k-1
由已证可知,当k-1为偶数即k为奇数时,存在m, 4m+9=3k成立 2分
当p=5时,则am+1+am+2+……+am+5=bk,即5am+3=bk
也即5(4m+13)=3k,而3k不是5的倍数,所以,当p=5时,所要求的m不存在
故不是所有奇数都成立. 2分


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
.(2009年上海卷理)如图,若正四棱柱![]() 的底面连长为2,高 为4,则异面直线
的底面连长为2,高 为4,则异面直线![]() 与AD所成角的大小是______________(结果用反三角函数表示).
与AD所成角的大小是______________(结果用反三角函数表示).

查看答案和解析>>
科目:高中数学 来源: 题型:
.(2009年上海卷理)如图,若正四棱柱![]() 的底面连长为2,高 为4,则异面直线
的底面连长为2,高 为4,则异面直线![]() 与AD所成角的大小是______________(结果用反三角函数表示).
与AD所成角的大小是______________(结果用反三角函数表示).
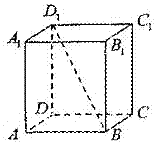
查看答案和解析>>
科目:高中数学 来源:2010届高三数学每周精析精练:概率 题型:填空题
(2009年上海卷理)某学校要从5名男生和2名女生中选出2人作为上海世博会志愿者,若用随机变量 表示选出的志愿者中女生的人数,则数学期望
表示选出的志愿者中女生的人数,则数学期望 ____________(结果用最简分数表示).
____________(结果用最简分数表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com