
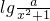 具有性质M,求a的取值范围;
具有性质M,求a的取值范围; (k≠0)、④y=ax(a>0且a≠1)、⑤y=logax(a>0且a≠1)的函数,指出哪些函数一定具有性质M?并加以证明.
(k≠0)、④y=ax(a>0且a≠1)、⑤y=logax(a>0且a≠1)的函数,指出哪些函数一定具有性质M?并加以证明. =
=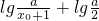
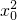 +1)=
+1)=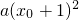 +a
+a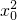 +2ax0+2a-2=0有实根…(5分)
+2ax0+2a-2=0有实根…(5分) ,满足题意
,满足题意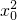 +2ax0+2a-2=0有实根有实根,只需满足△≥0,
+2ax0+2a-2=0有实根有实根,只需满足△≥0, ,3+
,3+ ]
] ,2)∪(2,3+
,2)∪(2,3+ ]…(8分)
]…(8分) ,3+
,3+ ]…(9分)
]…(9分)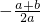 .
. (k≠0),则方程(*)可化为x2+x+1无解
(k≠0),则方程(*)可化为x2+x+1无解 (k≠0)不具备性质M;
(k≠0)不具备性质M;
 (k≠0),不恒具备性质M;
(k≠0),不恒具备性质M; (k≠0),不具备性质M;
(k≠0),不具备性质M; (k≠0)、④y=ax(a>0且a≠1)、⑤y=logax(a>0且a≠1)的函数,把其代入进行一一验证是否具有性质M;
(k≠0)、④y=ax(a>0且a≠1)、⑤y=logax(a>0且a≠1)的函数,把其代入进行一一验证是否具有性质M;

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:

A、{x|
| ||
B、{x|
| ||
| C、{x|1<x<2} | ||
| D、{x|1<x<5} |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题

 <x<4}
<x<4} <x<3}
<x<3}查看答案和解析>>
科目:高中数学 来源:2010年高考数学专项复习:不等式(解析版) 题型:选择题

 <x<4}
<x<4} <x<3}
<x<3}查看答案和解析>>
科目:高中数学 来源: 题型:
x | (-∞,-1) | -1 | (-1,0) | 0 | (0,1) | 1 | (1,+∞) |
y′ | - | 0 | + | 0 | - | 0 | + |
y | ↘ | 极小 | ↗ | 极大 | ↘ | 极小 | ↗ |
写出一个满足上表的函数___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com