
【题目】为了调查某省高三男生身高情况,现从某校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第一组![]() ,第二组
,第二组![]() ,…,第六组
,…,第六组![]() ,下图是按照上述分组方法得到的频率分布直方图.
,下图是按照上述分组方法得到的频率分布直方图.
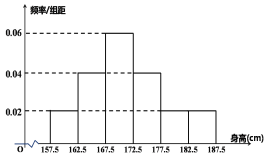
(1)求该学校高三年级男生的平均身高;
(2)利用分层抽样的方式从这50名男生中抽出20人,求抽出的这20人中,身高在177.5cm以上(含177.5cm)的人数;
(3)从根据(2)选出的身高在177.5cm以上(含177.5cm)的男生中任意抽取2人,求此二人来自于不同组的概率.
【答案】(1)171.5cm(2)4(3)![]()
【解析】
(1)结合频率分布直方图,求样本数据的平均值即可;
(2)利用分层抽样的方法,按比例抽取样本即可;
(3)由古典概型概率的求法,结合概率公式求解即可.
解:(1)由频率分布直方图可得:该学校高三年级男生的平均身高为
![]()
即该学校高三年级男生的平均身高为171.5cm;
(2)由频率分布直方图可知身高在177.5cm以上(含177.5cm)的概率为![]() ,
,
则利用分层抽样的方式从这50名男生中抽出20人,则抽出的这20人中,身高在177.5cm以上(含177.5cm)的人数为![]() 人;
人;
(3)由(2)可知,所抽取的4人中,![]() 2人,
2人,![]() 2人,
2人,
不妨设![]() 的2人编号为A,B,
的2人编号为A,B, ![]() 的2人编号为1,2,
的2人编号为1,2,
则从4人中抽取2人共有![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共6种不同取法,
共6种不同取法,
二人来自于不同组共有![]() ,
, ![]() ,
,![]() ,
,![]() 共4种不同取法,
共4种不同取法,
即二人来自于不同组的概率为![]() ,
,
故二人来自于不同组的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】某工厂有两个车间生产同一种产品,第一车间有工人200人,第二车间有工人400人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,并对他们中每位工人生产完成一件产品的时间(单位:min)分别进行统计,得到下列统计图表(按照[55,65),[65,75),[75,85),[85,95]分组).
分组 | 频数 |
[55,65) | 2 |
[65,75) | 4 |
[75,85) | 10 |
[85,95] | 4 |
合计 | 20 |
第一车间样本频数分布表
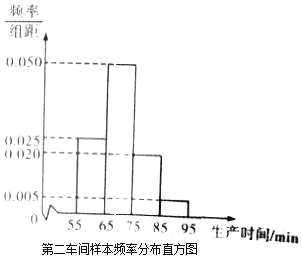
(Ⅰ)分别估计两个车间工人中,生产一件产品时间小于75min的人数;
(Ⅱ)分别估计两车间工人生产时间的平均值,并推测哪个车间工人的生产效率更高?(同一组中的数据以这组数据所在区间中点的值作代表)
(Ⅲ)从第一车间被统计的生产时间小于75min的工人中随机抽取2人,求抽取的2人中,至少1人生产时间小于65min的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品公司研发生产一种新的零售食品,从产品中抽取200件作为样本,测量这些产品的一项质量指标值,由测量结果得到如下的频率分布直方图:
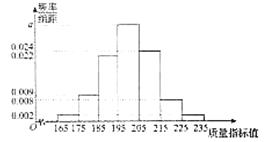
(1)求直方图中![]() 的值;
的值;
(2)由频率分布直方图可认为,这种产品的质量指标值![]() 服从正态分布
服从正态分布![]() ,试计算这批产品中质量指标值落在
,试计算这批产品中质量指标值落在![]() 上的件数;
上的件数;
(3)设产品的生产成本为![]() ,质量指标值为
,质量指标值为![]() ,生产成本与质量指标值满足函数关系式
,生产成本与质量指标值满足函数关系式![]() ,假设同组中的每个数据用该组数据区间的右端点代替,试计算生产该食品的平均成本.参考数据:若
,假设同组中的每个数据用该组数据区间的右端点代替,试计算生产该食品的平均成本.参考数据:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别是椭圆
分别是椭圆![]() 的左右焦点.
的左右焦点.
(Ⅰ)若![]() 是第一象限内该椭圆上的一点,
是第一象限内该椭圆上的一点,![]() ,求点
,求点![]() 的坐标.
的坐标.
(Ⅱ)若直线![]() 与圆
与圆![]() 相切,交椭圆
相切,交椭圆![]() 于
于![]() 两点,是否存在这样的直线
两点,是否存在这样的直线![]() ,使得
,使得![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年12月28日,成雅铁路开通运营,使川西多个市县进入动车时代,融入全国高铁网,这对推动沿线经济社会协调健康发展具有重要意义.在试运行期间,铁道部门计划在成都和雅安两城之间开通高速列车,假设每天7:00-8:00,8:00-9:00两个时间段内各发一趟列车由雅安到成都(两车发车情况互不影响),雅安发车时间及其概率如下表所示:
第一趟列车 | 第二趟列车 | |||||
发车时间 | 7:10 | 7:30 | 7:50 | 8:10 | 8:30 | 8:50 |
概率 | 0.2 | 0.3 | 0.5 | 0.2 | 0.3 | 0.5 |
若小王、小李二人打算乘动车从雅安到成都游玩,假设他们到达雅安火车站候车的时间分别是周六7:00和7:20(只考虑候车时间,不考虑其它因素).
(1)求小王候车10分钟且小李候车30分钟的概率;
(2)设小李候车所需时间为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com