练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．已知复数z1=1-i，z1z2=1+i，则z2=（　　）
    A．iB．-iC．1+iD．1-i

    分析 把z1=1-i代入z1z2=1+i，然后利用复数代数形式的乘除运算化简得答案．

    解答 解：∵数z1=1-i，z1z2=1+i，
    ∴${z}_{2}=\frac{1+i}{{z}_{1}}=\frac{1+i}{1-i}=\frac{（1+i）^{2}}{（1-i）（1+i）}=\frac{2i}{2}=i$．
    故选：A．

    点评 本题考查复数代数形式的乘除运算，是基础的计算题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    5．下列命题中，既是真命题又是特称命题的是（　　）
    A．有一个α，使tan（90°-α）=$\frac{1}{tanα}$
    B．存在实数x，使sinx=$\frac{π}{2}$
    C．对一切α，sin（180°-α）=sinα
    D．sin15°=sin60°cos45°-cos60°sin45°

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．【理】已知抛物线的方程为x2=2py（p＞0），过点A（0，-1）作直线l与抛物线相交于P，Q两点，点B的坐标为（0，1），连接BP，BQ，设BQ，BP与x轴分别相交于M，N两点．如果QB的斜率与PB的斜率的乘积为-3，则∠MBN的大小等于（　　）
    A．$\frac{π}{2}$B．$\frac{π}{4}$C．$\frac{π}{6}$D．$\frac{π}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知：a＞0，b＞0，不等式$a＞\frac{1}{x}＞-b$的解集是（　　）
    A．$\left\{{x\left|{-\frac{1}{b}＜x}\right.＜0或0＜x＜\frac{1}{a}}\right\}$B．$\left\{{x\left|{-\frac{1}{a}＜x}\right.＜0或0＜x＜\frac{1}{b}}\right\}$
    C．$\left\{{x\left|{x＜-\frac{1}{b}}\right.或x＞\frac{1}{a}}\right\}$D．$\left\{{x\left|{-\frac{1}{a}＜x}\right.＜\frac{1}{b}}\right\}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

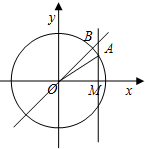    13．如图，角α的始边与x轴的非负半轴重合，终边与单位圆交于点A，直线MA垂直x轴于点M，B是直线y=x与MA的交点，设f（α）=$\overrightarrow{OA}•\overrightarrow{OB}$．
    （1）求f（α）的解析式；
    （2）若f（α）=$\frac{3}{5}$，求tanα的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．4个男生与3个女生站成一排，如果两端不站女生且3个女生必须相邻的排法有（　　）
    A．144种B．288种C．432种D．576种

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知两个等差数列{an}和{bn}的前n项和分别记为Sn和Tn，若$\frac{S_n}{T_n}=\frac{2n+1}{n+3}$，则$\frac{a_9}{b_9}$=（　　）
    A．$\frac{7}{4}$B．$\frac{3}{5}$C．$\frac{37}{21}$D．$\frac{19}{12}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知在△ABC中，cosA=-$\frac{5}{13}$，cosB=$\frac{3}{5}$．
    （Ⅰ）求sinC的值；
    （Ⅱ）设△ABC的面积S△ABC=$\frac{32}{5}$，求AB的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．在等差数列{an}中，若a1+a2+a3=32，a11+a12+a13=118，则a4+a10=（　　）
    A．45B．50C．75D．60

    查看答案和解析>>

    同步练习册答案