
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,以原点为极点,以![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(1)若曲线![]() 参数方程为:
参数方程为:![]() (
(![]() 为参数),求曲线
为参数),求曲线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)若曲线![]() 参数方程为:
参数方程为:![]() (
(![]() 为参数),
为参数),![]() ,且曲线
,且曲线![]() 与曲线
与曲线![]() 交点分别为
交点分别为![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,焦点在坐标轴上,且经过
的中心在原点,焦点在坐标轴上,且经过![]() ,
,![]() .
.
(Ⅰ)求椭圆的标准方程和离心率;
(Ⅱ)四边形![]() 的四个顶点都在椭圆
的四个顶点都在椭圆![]() 上,且对角线
上,且对角线![]() ,
,![]() 过原点
过原点![]() ,若
,若![]() ,求证:四边形
,求证:四边形![]() 的面积为定值,并求出此定值.
的面积为定值,并求出此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以原点
为参数).在以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列推理合理的是( )
A. 若函数y=f(x)是增函数,则f'(x)>0
B. 因为a>b(a,b∈R),则a+2i>b+2i(i是虚数单位)
C. A是三角形ABC的内角,若cosA>0,则此三角形为锐角三角形
D. α,β是锐角△ABC的两个内角,则sinα>cosβ
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】噪声污染已经成为影响人们身体健康和生活质量的严重问题,为了了解声音强度![]() (单位:分贝)与声音能量
(单位:分贝)与声音能量![]() (单位:
(单位:![]() )之间的关系,将测量得到的声音强度
)之间的关系,将测量得到的声音强度![]() 和声音能量
和声音能量![]() (
(![]() ,2,…,10)数据作了初步处理,得到如图散点图及一些统计量的值.
,2,…,10)数据作了初步处理,得到如图散点图及一些统计量的值.

表中![]() ,
,![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为声音强度
哪一个适宜作为声音强度![]() 关于声音能量
关于声音能量![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据表中数据,求声音强度![]() 关于声音能量
关于声音能量![]() 的回归方程;
的回归方程;
(3)当声音强度大于60分贝时属于噪音,会产生噪音污染,城市中某点![]() 共受到两个声源的影响,这两个声源的声音能量分别是
共受到两个声源的影响,这两个声源的声音能量分别是![]() 和
和![]() ,且
,且![]() .已知点
.已知点![]() 的声音能量等于声音能量
的声音能量等于声音能量![]() 与
与![]() 之和.请根据(1)中的回归方程,判断
之和.请根据(1)中的回归方程,判断![]() 点是否受到噪音污染的干扰,并说明理由.
点是否受到噪音污染的干扰,并说明理由.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
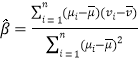 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是两个不同的平面,
是两个不同的平面,![]() 是两条不同的直线,有如下四个命题:
是两条不同的直线,有如下四个命题:
①若![]() ,则
,则![]() ; ②若
; ②若![]() ,则
,则![]() ;
;
③若![]() ,则
,则![]() ; ④若
; ④若![]() ,则
,则![]() .
.
其中真命题为_________(填所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有某高新技术企业年研发费用投入![]() (百万元)与企业年利润
(百万元)与企业年利润![]() (百万元)之间具有线性相关关系,近5年的年研发费用和年利润的具体数据如表:
(百万元)之间具有线性相关关系,近5年的年研发费用和年利润的具体数据如表:
年研发费用 |
|
|
|
|
|
年利润 |
|
|
|
|
|
数据表明![]() 与
与![]() 之间有较强的线性关系.
之间有较强的线性关系.
(1)求![]() 对
对![]() 的回归直线方程;
的回归直线方程;
(2)如果该企业某年研发费用投入8百万元,预测该企业获得年利润为多少?
参考数据:回归直线的系数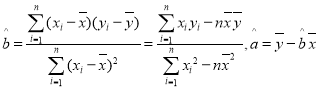 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com